Proposal for RISC‑V Matrix

Version 0.2-draft-20241128

This document explores design options for the RISC‑V Matrix extensions currently under discussion, including the Integrated Matrix Extension (IME) and the Attached Matrix Extension (AME). One particular method—accumulating the outer product of two vectors from the source matrixes into a tile of the destination matrix—is relevant for both IME and AME. There are elements of the IME and AME TG charters that need addressing to best exploit the strengths of outer product method, and this document explores why such an approach would be worth pursuing.

This proposal makes the assumption that the matrixes to be multiplied are quite large, and thus must be loaded incrementally. There are applications for matrix multiply by small matrixes that might be stored locally and used multiple times (e.g. a coordinate transform), but this proposal is not targeted at such applications.

Glossary

This document uses many concepts and acronyms from the RISC‑V Vector (RVV) extension. A simplified explanation of these items is given below for the reader not well-versed in RVV. The reader should refer to the RVV documentation for more precise definitions and explanations. Some other items are specific to these notes.

Δ: In these notes, Δ is the latency of addition in cycles. For integer generally Δ=1. For floating-point, Δ=4 is common for fp32, but may be less for less precise formats.
AME: The Attached Matrix Extension is a RISC‑V Task Group that aims to define high-performance matrix extensions for RISC‑V processors. This document proposes Outer Product Accumulators (OPA) as the basis for AME.
BF16: See bfloat16.
BLIS: BLIS is an acronym for BLAS-like Library Instantiation Software. See also BLIS (software).
CI: Computational Intensity (CI) is a metric for evaluating matrix extensions. It is defined as the number of element operations per element loaded.
DLEN: In these notes, DLEN is the Datapath width in bits (typically the number of vector operations per cycle is DLEN/SEW).
EEW: In RVV, EEW is an acronym for Effective Element Width in bits (see RISC‑V Vector Extension documentation). It is usually the width of vector instruction operand that is wider or narrower than SEW. EEW is used herein primarily as the width of the accumulation datatype.
EMUL: The Effective LMUL or Effective Length Multiplier specifies how many vector registers are required to hold the number of elements to operated on for a given vector operand. In this document it is generally LMUL×(EEW/SEW) for the operand.
fp16: Used in this document to refer to the IEEE 754 binary16 format (5‑bit exponent with 11 bits of precision).
fp32: Used in this document to refer to the IEEE 754 binary32 format (8‑bit exponent with 24 bits of precision).
fp4: Used in this document to refer to the OCP 4‑bit floating-point format, typically used with micro-scaling (e.g. an 8‑bit exponent for every 32 fp4 values).
fp8: Used in this document to refer to one of several proposed 8‑bit floating-point data types, e.g. binary8p3 (similar to OCP E5M2) or binary8p4 (similar to OCP E4M3).
IME: The Integrated Matrix Extension is a RISC‑V Task Group that aims to define incremental matrix extensions as a minimal addition to the RISC‑V Vector (RVV) instruction set. This document proposes OPA as a basis for IME to unify IME and AME, but the direction appears to be to have two incompatible extensions.
int8: Used in this document to refer to signed 8‑bit integers.
IPC: Instructions Per Cycle (IPC) is how many instructions a processor can execute per cycle, used herein as what can be sustained in the inner loop of matrix operations.
LMUL: In RVV, The Vector Length Multiplier (LMUL) is set by the vsetvli instruction. With LMUL=1, there are 32 vector registers of VLEN bits each. With LMUL>1 there are 32/LMUL vector registers of VLEN×LMUL bits each, i.e. LMUL>1 groups vector registers into larger entities. It can take the values 1, 2, 4, and 8.
MAC: This is an acronym for Multiply ACcumulate, e.g. a combined multiply and add, as in the operation acc ← acc + x×y. See also Multiply–accumulate operation.
MLEN: In these notes, MLEN is the Memory load width per cycle in bits. Typically MLEN=DLEN, but in some implementations it might differ. This set of notes sometimes uses MLEN, but also sometimes uses DLEN instead.
MVA: This set of notes refers to a specific IME proposal as MVA.
OCP: OCP is an acronym for Open Compute Project. It is only cited in this document for its OCP Microscaling Formats (MX) Specification, which specifies small scaled integer and floating-point formats such as MXFP8 (E5M2 or E4M3), MXFP6 (E3M2 or E2M3), MXFP4 (E2M1), and MXINT8.
OP: This is an abbreviation of operation, and is usually used in counting the number of multiplies and additions performed. Thus a MAC counts as two operations.
OPA: An acronym for Outer Product Accumulators, which is what these notes propose for AME at least, and perhaps for IME.
RVV: The RISC‑V Vector extension. This is the basis of IME and proposed as the basis for AME.
SEW: In RVV, SEW is an acronym for Selected Element Width in bits (see RISC‑V Vector Extension documentation). For example, setting SEW=8 via the vsetvli instruction causes most RVV instructions to operate on 8‑bit data for some source operands (widening operations make the destination twice as wide and narrowing operations make the destination half as wide).
TF32: See TensorFloat-32.
V: In these notes, V is used to represent the number of elements of a vector that can be loaded in a single cycle, i.e. V=MLEN/SEW.
VL: In RVV, VL is the name of a CSR, generally set by the vsetvli instruction with an upper bound of VLEN×LMUL/SEW, and is used to specify the number of elements operated on by a vector operation. Since this set of notes leaves things like matrix size not divisible by tile size as a detail for the reader, VL is primarily used herein for its maximum value.
VLEN: Vector register size in bits (see RISC‑V Vector Extension documentation).
VRF: In these notes, VRF denotes the RVV Vector Register File (32/LMUL vector registers of VLEN×LMUL bits). Register files are characterized by the number of entries, the width of those entries, and the number of read and write ports to entries of the file. Most VRF implementations have at least 4 read ports (3 for multiply/add instructions, 1 for stores) and 2 write ports (1 for multiply/add instructions, 1 for loads). In RVV, it is common for the vd operand, at least, to support access to a pair of entries for widening operations. Other operands might also support paired reads, and the number of such paired ports is critical to at least one IME proposal.

Proposal for RISC‑V Matrix

Matrix Multiply

Matrix Algebra

If $A$ is an $m \times n$ matrix and $B$ is an $n \times p$ matrix

A = (\begin{matrix} a_{1, 1} & a_{1, 2} & \dots & a_{1, n} \\ a_{2, 1} & a_{2, 2} & \dots & a_{2, n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m, 1} & a_{m, 2} & \dots & a_{m, n} \end{matrix}), B = (\begin{matrix} b_{1, 1} & b_{1, 2} & \dots & b_{1, p} \\ b_{2, 1} & b_{2, 2} & \dots & b_{2, p} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ b_{n, 1} & b_{n, 2} & \dots & b_{n, p} \end{matrix})

the matrix product $C = A B$ is defined to be the $m \times p$ matrix

C = (\begin{matrix} c_{1, 1} & c_{1, 2} & \dots & c_{1, p} \\ c_{2, 1} & c_{2, 2} & \dots & c_{2, p} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ c_{m, 1} & c_{m, 2} & \dots & c_{m, p} \end{matrix})

such that

c_{i, j} = a_{i, 1} b_{1, j} + a_{i, 2} b_{2, j} + \dots + a_{i, n} b_{n, j} = \sum_{k = 1}^{n} a_{i, k} b_{k, j}

Note that the above diagrams and equations work both when the elements are scalars or are themselves matrixes. For example, $c_{i, j}$ could be $r \times t$ matrix that is sum of the products of a column of $r \times s$ matrixes from $A$ with a row of $s \times t$ matrixes from $B$ . Such a submatrix is called a tile below. When a matrix multiplication is performed by tiles, typically the elements of $C$ are loaded into local storage, and all of the operations targeting that tile are performed, and then that local storage is written back to $C$ . In this scenario, each element of $C$ is read once and written once. In contrast, the elements of $A$ are read $p / t$ times and the elements of $B$ are read $m / r$ times. Larger tiles reduce references to memory and increase parallelism opportunities, but require more local storage.

Multiplying matrixes via tiles is illustrated in the following figure showing multiplying tiles from a column of of A with tiles from a row of B, accumulating to a tile of the product C:
Tile of C = Column of A times Row of B

Note also that software often transposes the $B$ prior to performing the matrix multiply, to avoided strided memory accesses for the columns of $A$ . This transpose is not reflected in the material below, and is left as an exercise to the reader.

The following exposition attempts to explain the reasoning for this proposal’s approach to matrix computation. In the following $N$ designates the problem matrix size, keeping these square for simplicity of exposition (e.g. the number of operations is simplified to $N^{3}$ rather than the more cumbersome $m \times p \times n$ ). Matrix multiply $C = C + A B$ is $N^{3}$ multiplications and $N^{3}$ additions with each matrix element $c_{i, j}$ being independent of the others but sequential due the additions. The $N^{3}$ multiplications are all independent (potentially done in parallel), but only $N^{2}$ of the additions are parallel when floating-point rounding is preserved. With unbounded hardware, the execution time of matrix multiply with floating-point rounding is $N \times Δ$ where $Δ$ is the add latency. This is achieved by using $N^{2}$ multiply/add units $N$ times every $Δ$ cycles, but a smarter implementation would use $N^{2} / Δ$ units pipelined to produce a value every cycle, thereby adding only $Δ - 1$ additional cycles for the complete result.

For practical implementation, hardware is bounded and should lay out in a regular fashion. Typically the number of multiply/add units is much smaller than $N$ , in which case there is flexibility in how these units are allocated to the calculations to be performed, but the allocation that minimizes data movement between the units and memory is to complete a tile of $C$ using the hardware array before moving on to a new tile. The computation that accomplishes this is the accumulation of the outer products [wikilink] of vectors from $A$ and $B$ . The goal is to determine the length of these vectors, and thus the size of the tile of $C$ . Below we use $T R$ for the tile rows and $T C$ for the tile columns, or just $T$ for a square $T \times T$ tile.

If $𝒖$ is a $m$ element vector and $𝒗$ is a $p$ element vector,

𝒖 = [\begin{matrix} u_{1} \\ u_{2} \\ ⋮ \\ u_{m} \end{matrix}], 𝒗 = [\begin{matrix} v_{1} \\ v_{2} \\ ⋮ \\ v_{p} \end{matrix}]

then the outer product is defined to be the $m \times p$ matrix

C = (\begin{matrix} c_{1, 1} & c_{1, 2} & \dots & c_{1, p} \\ c_{2, 1} & c_{2, 2} & \dots & c_{2, p} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ c_{m, 1} & c_{m, 2} & \dots & c_{m, p} \end{matrix}) = 𝒖 \otimes 𝒗 = (\begin{matrix} u_{1} v_{1} & u_{1} v_{2} & \dots & u_{1} v_{p} \\ u_{2} v_{1} & u_{2} v_{2} & \dots & u_{2} v_{p} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ u_{m} v_{1} & u_{m} v_{2} & \dots & u_{m} v_{p} \end{matrix})

i.e.

c_{i, j} = u_{i} v_{j}

The outer product is a fully parallel computation.

Using this formulation, the matrix product can be expressed as the sum of $n$ outer products of the columns of $A$ with the rows of $B$ :

C = A_{1 .. m, 1} \otimes B_{1, 1 .. p} + A_{1 .. m, 2} \otimes B_{2, 1 .. p} + \dots + A_{1 .. m, n} \otimes B_{n, 1 .. p} = \sum_{k = 1}^{n} A_{1 .. m, k} \otimes B_{k, 1 .. p}

where $A_{1 .. m, k}$ is column $k$ of $A$ and $B_{k, 1 .. p}$ is row $k$ of $B$ and $\otimes$ is the outer product operator.

For floating-point formats, the sums are typically done sequentially from 1 to $n$ to give the same rounding as the scalar implementation, which results in the latency $N \times Δ + Δ - 1$ when pipelined. The order of integer summation is not constrained, and is considerably faster, with $Δ \leq 1$ possible.

In most systems, the maximum tile size will either be a square power of two, e.g. 2×2, 4×4, 8×8, … 128×128, or a rectangle of a power of two and twice that, e.g. 4×2, 8×4, … 256×128. In a given problem, most of the operations will be done with the maximum tile size, with the remainder being the leftover edges. For example, with a maximum tile size of 64×64, a 1000×2000 by 2000×1500 multiplication yielding a 1000×1500 product would use tiles of 64×64 15×23=345 times with the last row of tiles being be 23 tiles of 40×64, the last column of tiles being 15 tiles of 64×28, and final corner would employ a 40×28 tile.

Matrix Multiply Using Vectors

The following series of transforms demonstrates how the simple, classic matrix multiply written as three nested loops shown below is transformed to for a vector ISA using outer products. (Note that the pseudo-code switches from 1‑origin indexing of Matrix Algebra to 0‑origin indexing of computer programming. Note also that, for clarity, the pseudo-code below does not attempt to handle the case of the matrix dimensions not being a multiple of the tile size.)

    for i ← 0 to m-1
      for j ← 0 to p-1
        for k ← 0 to n-1
          c[i,j] ← c[i,j] + a[i,k] * b[k,j]

The scalar version above would typically then move c[i,j] references to a register to reduce the load/store to multiply/add ratio from 4:1 to 2:1.

    for i ← 0 to m-1
      for j ← 0 to p-1
        acc ← c[i,j]
        for k ← 0 to n-1
          acc ← acc + a[i,k] * b[k,j]
        c[i,j] ← acc

However, in the vector version this step is delayed until after tiling. For vector, the above code is first tiled to become the following (here VL=VLEN/SEW):

    // iterate over 16×VL tiles of C
    for ti ← 0 to m-1 step 16
      for tj ← 0 to p-1 step VL
        // add product of sixteen columns of a (a[ti..ti+15,0..n-1])
        // and sixteen rows of b (b[0..n-1,tj..tj+VL-1]) to product tile
        for i ← 0 to 15
          for j ← 0 to VL-1
            for k ← 0 to n-1
              c[ti+i,tj+j] ← c[ti+i,tj+j] + a[ti+i,k] * b[k,tj+j]

The above code is then modified to use sixteen vector registers (EMUL≤1) as a 16×VL tile accumulator, and all i and j loops replaced by vector loads. (For VL=16 and EMUL≤1, this requires VLEN≥128 for 8‑bit C data, 256 for 16‑bit C data, 512 for 32‑bit C data, and 1024 for 64‑bit C data. For widening multiply/adds (EMUL=2*LMUL) where LMUL=1 and EMUL=2, only 8×VL tiles may be used as the destination will be even/odd register pairs.)

    for ti ← 0 to m-1 step 16		// tile i
      for tj ← 0 to p-1 step VL		// tile j
	// copy to accumulator
	v0  ← c[ti+ 0,tj..tj+VL-1]	// 16 VL-element vector loads
	v1  ← c[ti+ 1,tj..tj+VL-1]	// to use vector registers
	v2  ← c[ti+ 2,tj..tj+VL-1]	// as an 16×VL accumulator
	v3  ← c[ti+ 3,tj..tj+VL-1]
	⋮
	v15 ← c[ti+15,tj..tj+VL-1]
	// add product of a[ti..ti+15,0..n-1]
	// and b[0..n-1,tj..tj+VL-1] to tile
	for k ← 0 to n-1
	  va  ← a[ti..ti+i+15,k]		// 16-element vector load
	  vb  ← b[k,tj..tj+i+VL-1]	// VL-element vector load
	  v0  ← v0  + a[ti+ 0,k] * vb	// vector * scalar
	  v1  ← v1  + a[ti+ 1,k] * vb
	  v2  ← v2  + a[ti+ 2,k] * vb
	  v3  ← v3  + a[ti+ 3,k] * vb
	  ⋮
	  v15 ← v15 + a[ti+15,k] * vb
	// copy accumulator back to tile
	c[ti+ 0,tj..tj+VL-1] ←  v0	// 16 VL-element vector stores
	c[ti+ 1,tj..tj+VL-1] ←  v1	// to store accumulator
	c[ti+ 2,tj..tj+VL-1] ←  v2	// back to C tile
	c[ti+ 3,tj..tj+VL-1] ←  v3
	⋮
	c[ti+15,tj..tj+VL-1] ← v15

The inner loop has:

1 vector load (VLEN bits each), taking VLEN/MLEN cycles;
16 scalar loads (SEW bits each);
16 vector-scalar multiply/add instructions, each taking VLEN/DLEN cycles;
and 24 integer instructions

This is a total of 57 instructions; a combination of IPC ≥ 2 and VLEN/DLEN > 1 is required to achieve VL multiply/adds per cycle.

One limitation of the RISC‑V vector instruction set is the lack of a vector × scalar instruction where the scalar is an element of a vector register. Extending the RISC‑V Vector instruction set would save many scalar loads and address adds in the above loop, but would require an efficient strided vector load or transposing the A matrix.

For SEW < 64 a different possible addition to the RISC‑V Vector (RVV) instruction set would be a vector-scalar multiply/accumulate that takes the scalar from an offset in the scalar register. It is then possible to pack 64/SEW (2, 4, or 8) values into f or x registers by loading with FLD or LD, and then the extension would allow .vf or .vx to specify a 3-bit immediate specifying which portion of the scalar register register to use as the scalar operand (and disabling the RISC‑V NaN-boxing check for this packed SIMD reference). This might require a wider vector instruction word. Given the stride on the scalar loads, this SIMD packing would require unrolling the k loop 64/SEW times. The primary advantage of such an extension is the application to matrix-vector products.

Computational intensity is defined as the ratio of the number of element-level multiply/add operations to the number of elements loaded. The vector code above performs $16 VL$ multiply/adds for $16 + VL$ elements loaded. For example, this is a computational intensity of 8, 10.7, and 12.8 for VL values 16, 32, and 64 respectively.

The vector code above requires $16 VL + 16 + VL$ elements of register storage.

Besides the obvious parallelism advantage, another improvement is that each element of the $A$ and $B$ matrixes is used sixteen times per load, which improves energy efficiency. However, one limitation of the vector implementation of matrix multiply is the limited number of multiply/add units that can be used in parallel. It is obvious that the above can use VL units in parallel (one for each element of the vectors). Slightly less obvious is that for VL=16 an implementation could employ $256 / Δ$ units to execute the above code, issuing groups of $16 / Δ$ vector instructions in a single cycle, and parceling these vector operations out to the various units to proceed in parallel. After $16 / Δ$ instructions, the next group can be issued to the pipelined units. It would be necessary to provide substantial additional Vector Register File (VRF) bandwidth to support this. If instruction issue is limiting, an instruction that packaged groups of the above vector operations could be provided. Given this observation, there are three reasons to add a more robust matrix extension to RISC‑V:

To obtain better energy efficiency on the computation by reducing the data movement in the above, particularly the VRF bandwidth.
To allow even more multiply/add units to be employed on matrix operations (the above limited to 30×VL tiles by the number of vector registers, as it uses 2 of the 32 vector registers for va and vb).
To support EEW/SEW > 2 for SEW=8 or SEW=4 and EEW=32 (i.e. quad-widening and octo-widening).

The next sections introduce a possible Integrated Matrix Extension that accomplishes all three of the above goals.

While it is obvious, for reference, the following pseudo-code gives the widening form of the RVV matrix multiply (LMUL=1 EMUL=2).

    for ti ← 0 to m-1 step 8		// tile i
      for tj ← 0 to p-1 step VL		// tile j
        // copy to accumulator
        v0  ← c[ti+0,tj..tj+VL-1]		// 8 VL-element vector loads (LMUL=2)
        v2  ← c[ti+1,tj..tj+VL-1]		// to use vector register pairs
        v4  ← c[ti+2,tj..tj+VL-1]		// as an 8×VL accumulator
        v6  ← c[ti+3,tj..tj+VL-1]
        v8  ← c[ti+4,tj..tj+VL-1]
        v10 ← c[ti+5,tj..tj+VL-1]
        v12 ← c[ti+6,tj..tj+VL-1]
        v14 ← c[ti+7,tj..tj+VL-1]
        // add product of a[ti..ti+7,0..n-1]
        // and b[0..n-1,tj..tj+VL-1] to tile
        for k ← 0 to n-1
	  vb  ← b[k,tj..tj+i+VL-1]	// VL-element vector load
	  v0  ← v0  + a[ti+0,k] * vb	// vector * scalar
	  v2  ← v2  + a[ti+1,k] * vb
	  v4  ← v4  + a[ti+2,k] * vb
	  v6  ← v6  + a[ti+3,k] * vb
	  v8  ← v8  + a[ti+4,k] * vb
	  v10 ← v10 + a[ti+5,k] * vb
	  v12 ← v12 + a[ti+6,k] * vb
	  v14 ← v14 + a[ti+7,k] * vb
        // copy accumulator back to tile
        c[ti+ 0,tj..tj+VL-1] ←  v0	// 8 VL-element vector stores
        c[ti+ 1,tj..tj+VL-1] ←  v2
        c[ti+ 2,tj..tj+VL-1] ←  v4
        c[ti+ 3,tj..tj+VL-1] ←  v6
        c[ti+ 4,tj..tj+VL-1] ←  v8
        c[ti+ 5,tj..tj+VL-1] ← v10
        c[ti+ 6,tj..tj+VL-1] ← v12
        c[ti+ 7,tj..tj+VL-1] ← v14

Matrix Multiply Using An Outer Product Array

It is desirable to match the number of multiply/add units to the load bandwidth when practical, as this results in a balanced set of resources (memory and computation are equally limiting). We use $V$ to represent the vector load bandwidth as the number of elements per cycle. Assuming that loads and computation are done in parallel, next we ask what is the tile size that balances results in equal time loading and computing. We have already seen that the multiply/adds in a matrix multiply is O(N³) but with O(N²) parallelism, so the time can be made as fast as O(N). However loading the data from memory is O(N²), so with sufficient hardware, data load time will be O(N) times the compute time. When load time grows quadratically with problem size while compute time grows linearly, a balanced system will scale up the compute hardware to match the load bandwidth available but not go any further. Of course, to achieve O(N) compute time requires O(N²) hardware, which is feasible for typical T×T matrix tiles, but usually not for the entire problem size N. Conversely, for balanced systems, when load bandwidth increases linearly, the computation array increases quadratically.

Since a vector load provides $V$ elements in a single cycle, it makes sense to find the tile size that matches this load bandwidth. This turns out to be a tile of $V \times V$ . This tile can be computed by $V$ outer products. Take one cycle to load $V$ elements from $A$ and one cycle to load $V$ elements from $B$ . Processing these values in two cycles matches load bandwidth to computation. For $Δ \leq 2$ , a $V \times (V / 2)$ array of multiply/add units with $V^{2}$ accumulators (two per multiply/add unit) accomplishes this by taking the outer product of all of the $𝒖$ vector (from $A$ ) and the even elements of the $𝒗$ vector (from $B$ ) in the first cycle, and all of $𝒖$ with the odd elements of $𝒗$ in the second cycle. The full latency is $Δ + 1$ cycles, but with pipelining a new set of values can be started every two cycles. For $Δ > 2$ , using a $V \times (V / Δ)$ pipelined array for $Δ$ cycles is a natural implementation but does not balance load cycles to computation cycles. For example, for $Δ = 4$ , a $V \times (V / 4)$ array completes the outer product in 4 cycles, which is half of the load bandwidth limit. For $Δ = 4$ there are multiple ways to match the load bandwidth and adder latency. A good way would be to target a $2 V \times 2 V$ accumulation tile taking four load cycles and four computation cycles, but this requires $4 V^{2}$ accumulators, with four accumulators for each multiply/add unit. The method that minimizes hardware is to process two tiles of $C$ in parallel using pipelined multiply/add units by doing four cycles of loads followed by two 2‑cycle outer products to two sets of $V^{2}$ accumulators. For example, the loads might be $V$ elements from an even column of $A$ , $V$ elements from an even row of $B$ , $V$ elements from an odd column of $A$ , and $V$ elements from an odd row of $B$ . The computation would consist of two $V \times (V / 2)$ outer product accumulates, each into $V^{2}$ accumulators (total $2 V^{2}$ ). The total latency is seven cycles but the hardware is able to start a new outer product every four cycles by alternating the accumulators used, thereby matching the load bandwidth. If any of these array sizes is too large for the area budget, then it will be necessary to reduce performance, and no longer match the memory hierarchy. However, in 2024 process nodes (e.g. 3 nm), it would take fairly large $V$ to make the multiply/add unit array visible on a die.

A $V \times V$ multiply/add array with one accumulator per unit is illustrated below for $V = 4$ :
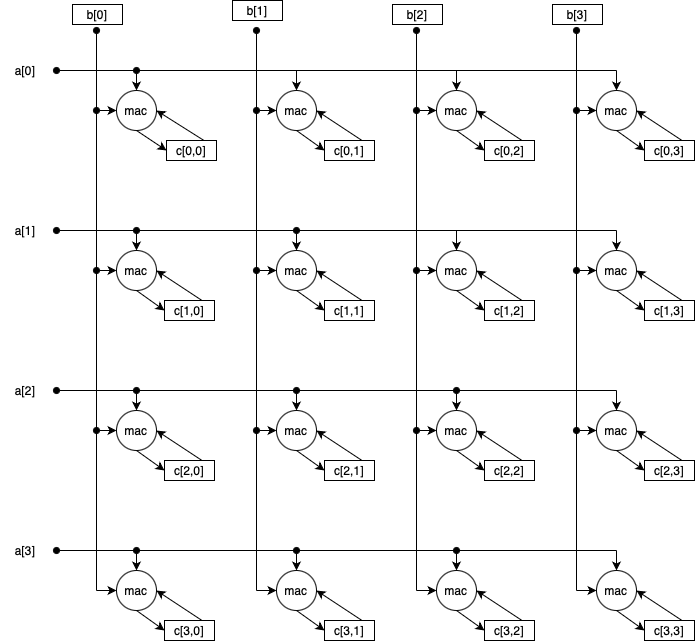
4×4 Outer Product Array with Local Accumulators

The above array is not suggested for use, as compute exceeds the load bandwidth. Instead one proposal developed above is a $V \times (V / 2)$ multiply/add array with two accumulators per unit for two cycle accumulation to $V \times V$ accumulators. This is illustrated below for $V = 4$ :
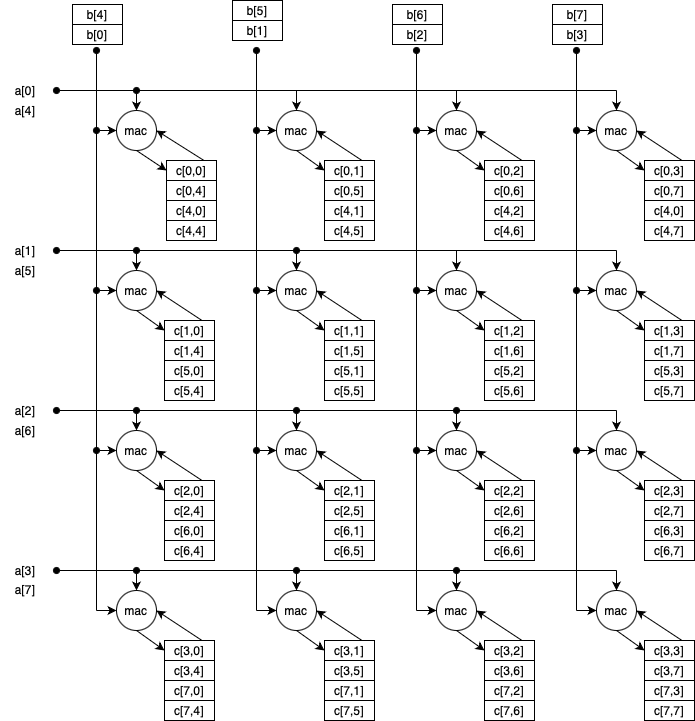
4×2 Outer Product Array with 4×4 Accumulators

A $V \times V$ multiply/add array with four accumulators per unit for $2 V \times 2 V$ accumulation is illustrated below for $V = 4$ . Such an array would be used four times over four cycles, each cycle sourcing from a different combination of $V$ elements from the $2 V$ elements loaded from A and the $2 V$ elements loaded from B. This is one possibility explained above for supporting $Δ = 4$ or simply to improve performance energy efficiency for $Δ \leq 2$ .
4×4 Outer Product Array with 8×8 Accumulators

The $V \times (V / 2)$ sequence for $Δ = 2$ is illustrated below, using superscripts to indicate cycle numbers, as in $C^{0} = 0$ to indicate accumulators being zero on cycle 0, $𝒖^{0}$ the value loaded on cycle 0, $𝒗^{1}$ the vector loaded on cycle 1, $C^{3}$ the result of the first half of the two-cycle latency outer product, $C^{4}$ the result of the second half of the outer product, etc.

C^{0} = (\begin{matrix} 0 & \dots & 0 \\ ⋮ & ⋱ & ⋮ \\ 0 & \dots & 0 \end{matrix}), 𝒖^{0} = [\begin{matrix} a_{1, 1} \\ a_{2, 1} \\ ⋮ \\ a_{m, 1} \end{matrix}], 𝒗^{1} = [\begin{matrix} b_{1, 1} \\ b_{1, 2} \\ ⋮ \\ b_{1, p} \end{matrix}], 𝒖^{2} = [\begin{matrix} a_{1, 2} \\ a_{2, 2} \\ ⋮ \\ a_{m, 2} \end{matrix}], 𝒗^{3} = [\begin{matrix} b_{2, 1} \\ b_{2, 2} \\ ⋮ \\ b_{2, p} \end{matrix}],

C^{3} = C^{0} + 𝒖^{0} \otimes 𝒖^{1} = (\begin{matrix} u_{1}^{0} v_{1}^{1} & 0 & \dots & u_{1}^{0} v_{p - 1}^{1} & 0 \\ u_{2}^{0} v_{1}^{1} & 0 & \dots & u_{2}^{0} v_{p - 1}^{1} & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ u_{m}^{0} v_{1}^{1} & 0 & \dots & u_{m}^{0} v_{p - 1}^{1} & 0 \end{matrix}) = (\begin{matrix} a_{1, 1} b_{1, 1} & 0 & \dots & a_{1, 1} b_{1, p - 1} & 0 \\ a_{2, 1} b_{1, 1} & 0 & \dots & a_{2, 1} b_{1, p - 1} & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ a_{m, 1} b_{1, 1} & 0 & \dots & a_{m, 1} b_{1, p - 1} & 0 \end{matrix}),

C^{4} = (\begin{matrix} u_{1}^{0} v_{1}^{1} & u_{1}^{0} v_{2}^{1} & \dots & u_{1}^{0} v_{p - 1}^{1} & u_{1}^{0} v_{p}^{1} \\ u_{2}^{0} v_{1}^{1} & u_{2}^{0} v_{2}^{1} & \dots & u_{2}^{0} v_{p - 1}^{1} & u_{2}^{0} v_{p}^{1} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ u_{m}^{0} v_{m}^{1} & u_{m}^{0} v_{m}^{1} & \dots & u_{m}^{0} v_{p - 1}^{1} & u_{m}^{0} v_{p}^{1} \end{matrix}) = (\begin{matrix} a_{1, 1} b_{1, 1} & a_{1, 1} b_{1, 2} & \dots & a_{1, 1} b_{1, p - 1} & a_{1, 1} b_{1, p} \\ a_{2, 1} b_{1, 1} & a_{2, 1} b_{1, 2} & \dots & a_{2, 1} b_{1, p - 1} & a_{2, 1} b_{1, p} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ a_{m, 1} b_{1, 1} & a_{m, 1} b_{1, 2} & \dots & a_{m, 1} b_{1, p - 1} & a_{m, 1} b_{1, p} \end{matrix}),

C^{5} = (\begin{matrix} c_{1, 1}^{3} + u_{1}^{2} v_{1}^{3} & c_{1, 2}^{4} & \dots & c_{1, p -1}^{3} + u_{1}^{2} v_{p - 1}^{3} & c_{1, p}^{4} \\ c_{2, 1}^{3} + u_{2}^{2} v_{1}^{3} & c_{2, 2}^{4} & \dots & c_{2, p -1}^{3} + u_{2}^{2} v_{p - 1}^{3} & c_{2, p}^{4} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ c_{m, 1}^{3} + u_{m}^{2} v_{1}^{3} & c_{m, 2}^{4} & \dots & c_{m, p -1}^{3} + u_{m}^{2} v_{p - 1}^{3} & c_{m, p}^{4} \end{matrix}),

C^{6} = (\begin{matrix} c_{1, 1}^{5} & c_{1, 2}^{4} + u_{1}^{2} v_{2}^{3} & \dots & c_{1, p -1}^{5} & c_{1, p}^{4} + u_{1}^{2} v_{p}^{3} \\ c_{2, 1}^{5} & c_{2, 2}^{4} + u_{2}^{2} v_{2}^{3} & \dots & c_{2, p -1}^{5} & c_{2, p}^{4} + u_{2}^{2} v_{p}^{3} \\ ⋮ & ⋮ & ⋱ & ⋮ & ⋮ \\ c_{m, 1}^{5} & c_{m, 2}^{4} + u_{m}^{2} v_{2}^{3} & \dots & c_{m, p -1}^{5} & c_{m, p}^{4} + u_{m}^{2} v_{p}^{3} \end{matrix}), \dots

The following series of transforms demonstrates how the simple, classic matrix multiply written as three nested loops shown below is transformed to use tiles with an outer product multiply/add/accumulator array. For the tiling, usually TR=TC=V or TR=TC=2V, but there may be implementations that choose other vector lengths for microarchitectural reasons, and this should be supported.

    for i ← 0 to m-1
      for j ← 0 to p-1
        for k ← 0 to n-1
          c[i,j] ← c[i,j] + a[i,k] * b[k,j]

The above code is then tiled to become the following:

    // iterate over TR×TC tiles of C
    for ti ← 0 to m-1 step TR
      for tj ← 0 to p-1 step TC
        // add product of a[ti..ti+TR-1,0..n-1]
        // and b[0..n-1,tj..tj+TC-1] to tile
        for i ← 0 to TR-1
          for j ← 0 to TC-1
            for k ← 0 to n-1
              c[ti+i,tj+j] ← c[ti+i,tj+j] + a[ti+i,k] * b[k,tj+j]

The above code is modified to use an accumulator:

    for ti ← 0 to m-1 step TR
      for tj ← 0 to p-1 step TC
        // copy to accumulator
        for i ← 0 to TR-1
          for j ← 0 to TC-1
            acc[i,j] ← c[ti+i,tj+j]
        // add product of a[ti..ti+TR-1,0..n-1]
        // and b[0..n-1,tj..tj+TC-1] to tile
        for i ← 0 to TR-1
          for j ← 0 to TC-1
            for k ← 0 to n-1
              acc[i,j] ← acc[i,j] + a[ti+i,k] * b[k,tj+j]
        // copy accumulator back to tile
        for i ← 0 to TR-1
          for j ← 0 to TC-1
            c[ti+i,tj+j] ← acc[i,j]

The above code is then vectorized by moving the k loop outside:

    for ti ← 0 to m-1 step TR
      for tj ← 0 to p-1 step TC
        for i ← 0 to TR-1
          acc[i,0..TC-1] ← c[ti+i,tj..tj+TC-1]    // TC-element vector load + acc write
        for k ← 0 to n-1
          va ← a[ti..ti+i+TR-1,k]                 // TR-element vector load
          vb ← b[k,tj..tj+i+TC-1]                 // TC-element vector load
          acc ← acc + outerproduct(va, vb)        // 2-cycle outer product instruction
        for i ← 0 to TR-1
          c[ti+i,tj..tj+TC-1] ← acc[i,0..TC-1]    // acc read + TC-element vector store

where the outerproduct instruction is defined as follows:

        for i ← 0 to va.length-1
          for j ← 0 to vb.length-1
            acc[i,j] ← acc[i,j] + va[i] * b[j]

The above performs $T R \times T C$ multiply/adds for $T R + T C$ elements loaded. For a square tile $T \times T$ , this is a computational intensity of $T / 2$ , and for the rectangular tile $2 T \times T$ , this is a computational intensity of $2 T / 3$ , which is slightly better than the square case. Compared to the earlier vector method, this has identical computational intensity for the same tile sizes, but which is not limited by the number of vector registers (it uses only two), and thus may grow as large as value of $T$ the implementation chooses to support.

The vector code above performs $T R \times T C$ multiply/adds for $T R \times T C + T R + T C$ elements stored. Compared to the earlier vector method, this has identical storage requirement for the same tile sizes. However, accumulator storage is much cheaper than vector register file storage, which is not reflected in the storage requirement. Also, this method supports much larger $T R$ and $T C$ , which at larger sizes is almost entirely distributed, low-power accumulator storage.

In the Matrix Algebra section it was observed that cycle count for matrix multiplication with the smarter variant of unbounded multiply/add units (i.e. $N^{2} / Δ$ units) pipelined to produce a value every cycle takes $N \times Δ + Δ - 1$ cycles. It is worth answering how the above method fares relative to this standard applied to a single tile. Because we cut the number of multiply/add units in half to match the load bandwidth, we expect at least twice the cycle count, and this expectation is met: matching a memory system that delivers $V$ elements per cycle, a tile of $V \times V$ processed by an array of $V \times (V / 2)$ multiply/add units ( $Δ \leq 2$ ) produces the tile in $2 V + 1$ cycles. It may help to work an example. For a memory system delivering one 512‑bit cache block per cycle and 16‑bit data (e.g. BF16), $V = 32$ , and the 32×32 tile is produced using 2 vector loads and one 2‑cycle outer product instruction iterated 32 times taking 64 cycles yielding 512 multiply/adds per cycle. However, this does not include the time to load the accumulators before and transfer them back to $C$ after. When this 64 cycle tile computation is part of a 1024×1024 matrix multiply, this tile loop will be called 32 times for each tile of $C$ . If it takes 64 cycles to load the accumulators from memory and 64 cycles to store back to memory, then this is 64+32×64+64=2176 total cycles. There are a total of 1024 output tiles, so the matrix multiply is 2228224 cycles (not counting cache misses) for 1024³ multiply/adds, which works out to 481.88 multiply/adds per cycle, or 94% of peak.

Note that there is no point in loading entire tiles, as this would not benefit performance. Rows and columns are loaded and consumed, and not used again. Storing whole tiles of the $A$ and $B$ matrixes would only be useful in situation when such a tile is used repeatedly, which does not occur in a larger matrix multiply. This does occur for the accumulation tile of the $C$ matrix, which does make that worth storing locally. The question is where it should be stored.

Matrix Accumulators

The bandwidth of reads and writes to outer product accumulators far exceeds what a Vector Register File (VRF) generally targets, which suggests that that these structures be kept separate. Also the number of bits in the accumulators is potentially large relative to VRF sizes. Increasing the bandwidth and potentially the size of the VRF to meet the needs of outer product accumulation is not a good solution. Rather the accumulator bits should located in the multiply/add array, and be transferred to memory when a tile is completed. This transfer might be one row at a time through the VRF, since the VRF has the necessary store operations and datapaths to the cache hierarchy. The appropriateness of separate accumulator storage may be illustrated by examples. A typical vector load width might be the cache block size of 512 bits. This represents 64 8‑bit elements. If the products of these 8‑bit elements is accumulated in 16 bits (e.g. int16 for int8 or fp16 for fp8), then for $Δ \leq 2$ , 16×64² = 65536 bits of accumulator are required. The entire VRF might need only half as many bits, and these bits require more area than accumulator bits, as the VRF must support at least 4 read ports and 2 write ports for parallel execution of vmacc.vv and a vector load or vector store. If vector registers are renamed, then VRF bits are even more costly. In contrast, accumulator storage within the multiply/add array is local, small, and due to locality consumes negligible power. As another example, consider the same 512 bits as sixteen IEEE 754 binary32 elements with $Δ = 4$ . The method for this latency suggests a 16×8 array of binary32 multiply/add units with 2048 32‑bit accumulators, which is again a total of 65536 bits of accumulator storage, but now embedded in much larger multiply/add units.

The number of bits require for accumulation needs to be determined (the example above is not meant to be anything other than an example). Recently the TF32 format appears to be gaining popularity for AI applications, and so accumulation in TF32 for BF16 inputs is one option. However, this needs further investigation.

Making Outer Product Scalable

An outer product instruction is an easy addition to the RISC‑V vector extension, but it needs be made scalable. Accumulators are defined to be 32 bits with an option to use pairs of accumulators for 64‑bit data. The primary parameter for implementations to choose will be the number of accumulators. This will be a square T×T array for holding a tile of the C matrix up to this size. Implementations will then choose the number of multiply/add units that are used to calculate the inner product of vectors of T elements. For example, this document explored choosing T=V for load bandwidth matching for Δ≤2 and T=2V for Δ=4, but an implementation might choose a smaller T value to reduce the hardware cost, or a reduced number of multiply/add units, or both. Typically these units would also be organized as an array of M×N units. In this case there are $T^{2} / M N$ accumulators per unit.

The number of rows and columns in the C tile may be less than T. The number of tile columns is less than T when processing the last column of tiles when p is not a multiple of T. The number of tile rows is less than T when processing the last row of tiles of C when m is not a multiple of T. Software is expected to use the msetcli instruction to set the TR CSR to the number of rows in the C tile as min(x[rs1], T×LMUL), and to use the msetrli instruction to set the TC CSR to the number of columns in the C tile as min(x[rs1], T×LMUL).

Most of the C matrix (i.e except at its right and bottom edges), will be processed with TR = T and TC = T. Here a loop iterated T times will load vectors from the A and B matrixes into two vector registers (e.g. va and vb) and the instruction vouteracc.avv va, vb used to accumulate the outer product of these vectors as shown in the following example for 8-bit data, which assumes that the A and B has been packed as in BLIS for in-stride access:

loop:
	vle8.v	va, (ra);	add	ra, ra, rt
	vle8.v	vb, (rb);	add	rb, rb, rt
	vfouteracc.avv va, vb;	bne	ra, rn, loop

The packing required is implementation-specific, and should be determined by use of a msetcli/msetrli pair of instructions.

When TR ≠ TC software will use a different loop that loads TR elements from A and TC elements from B. This will involve setting VL to these two values in the loop rather than outside of the loop, and will require more instructions as a result. Some amount of unrolling may amortize the writes to VL, e.g. setting VL to TR and doing four loads from A, then setting setting VL to TC and doing four loads from B, and then doing four outer products.

This proposal implements the above by using the existing RVV VL CSR to hold the number of tile columns, and adds a TR CSR for the number of tile rows. These are set by the msetcli/msetrli pair of instructions that set VL and TR for columns and rows in an analogous fashion to vsetvli.

The msetcli/msetrli instructions set VL and TR to the minimum of target lengths for their outer product instruction and their rs1 argument. For some implementations the target rows and columns will be chosen to be the larger of the hardware array rows and columns and $V$ , the number of elements that can be loaded in a single cycle. Other implementations may choose some multiple of $V$ instead, and then iterate as shown below for a square hardware array:

        for k ← 0 to VL step T
          acc ← acc + outerproduct(va[k..min(k+T-1,TR)], vb[k..min(k+T-1,VL)])

or as shown below for a rectangle hardware array:

        ka ← 0
	kb ← 0
	while ka < TR & kb < VL
          acc ← acc + outerproduct(va[ka..min(ka+TR-1,TR)], vb[kb..min(kb+TC-1,VL)])
          ka ← ka + TR
          kb ← kb + TC

For msetcli/msetrli to set the appropriate values, it will be necessary to add a floating-point flag. For integer, usually Δ=1 (and Δ<1 is possible with carry-save arithmetic), but floating-point may have 2≤Δ≤4 depending on SEW, and earlier it was seen that Δ≤2 and Δ=4 might be handled differently.

Specifics of the Proposal

At a high-level, this proposal would add state and instructions along the lines of the following to the RISC‑V Vector Extension. The details would be developed as appropriate if this general approach is accepted for further development.

A goal of the following is to allow the microarchitecture to provide whatever size outer product array is appropriate for a given SEW (and thus V) and Δ. This could be either larger or smaller than values suggested in this document. In addition the microarchitecture, by setting VL and TR can determine how much to load from memory for the v*outeracc.avv instructions, for example, using a longer load for Δ=4 as suggested earlier, or to do multiple outer product accumulations to the same accumulators.

CSRs
- acccolb is a read-only CSR, analogous to vlenb, specifying the whole register read length in bytes for one row of the accumulators.
- accrows is a read-only CSR that specifies how many rows of accumulator state exist and is used to direct context switch.
- TR is a CSR that specifies the number of elements to read from the vs1 operand of vouter*.avv and vfouter*.avv instructions and the number of accumulator rows to update. (The existing VL CSR specifies the number of elements to read from the vs2 operand of vouter*.avv and vfouter*.avv instructions and the number of accumulator columns to update.)
Register Array
- acc is an implementation-specific amount of state use to accumulate outer products in an implementation-specific format. For context switch purposes it consists of accrows of acccolb bytes. For other purposes, the number of rows and columns are determined by SEW, VL, and TR.
Instructions
- msetcli rd, rs1, vtypei sets VL based on the number of columns specified in rs1 that can be processed by the v*outer*.avv instructions and returns this value to rd.
- msetrli rd, rs1, vtypei sets TR based on the number of rows specified in rs1 that can be processed by the v*outer*.avv instructions and returns this value to rd.
- vouter.avv vs1, vs2 performs an integer widening outer product (acc ← outerproduct(vs1, vs2)) for the current settings of SEW, VL, and TR. Only VL columns and TR rows of the accumulators are modified. The accumulators are 32 bits in width, with pairs used when SEW=32. SEW=64 is not supported.
- vouteracc.avv vs1, vs2 performs an integer widening outer product (acc ← acc + outerproduct(vs1, vs2)) for the current settings of SEW, VL, and TR. Only VL columns and TR rows of the accumulators are modified. The accumulators are 32 bits in width, with pairs used when SEW=32. SEW=64 is not supported.
- vfouter.avv vs1, vs2 performs a floating-pointer outer product (acc ← outerproduct(vs1, vs2)) for the current settings of SEW, VL, and TR. Only VL columns and TR rows of the accumulators are modified.
- vfouteracc.avv vs1, vs2 performs a floating-pointer outer product accumulate (acc ← acc + outerproduct(vs1, vs2)) for the current settings of SEW, VL, and TR. Only VL columns and TR rows of the accumulators are modified.
- vraccr vd, rs1 reads the row of acc selected by rs1 and writes this to vd in the integer format selected by SEW using the length specified by VL. This transfer may involve some format conversion from the internal accumulator format to the specified integer format.
- vraccc vd, rs1 reads the column of acc selected by rs1 and writes this to vd in the integer format selected by SEW using the length specified by TR. This transfer may involve some format conversion from the internal accumulator format to the specified integer format.
- vfraccr vd, rs1 reads the row of acc selected by rs1 and writes this to vd in the floating-point format selected by SEW using the length specified by VL. This transfer may involve some format conversion from the internal accumulator format to the specified floating-point format.
- vfraccc vd, rs1 reads the column of acc selected by rs1 and writes this to vd in the floating-point format selected by SEW using the length specified by TR. This transfer may involve some format conversion from the internal accumulator format to the specified floating-point format.
- vrraccr vd, rs1 reads the raw format row of acc selected by rs1 and writes this to vd as bytes as determined by acccolb.
- vwaccr rs1, vs2 writes the row of acc selected by by rs1 from vs2 in the integer format selected by SEW using the length specified by VL. This transfer may involve some format conversion to the internal accumulator format from the specified integer format.
- vwaccc rs1, vs2 writes the column of acc selected by by rs1 from vs2 in the integer format selected by SEW using the length specified by TR. This transfer may involve some format conversion to the internal accumulator format from the specified integer format.
- vfwaccr rs1, vs2 writes the row of acc selected by rs1 from vd in the floating-point format selected by SEW using the length specified by VL. This transfer may involve some format conversion to the internal accumulator format from the specified floating-point format.
- vfwaccc rs1, vs2 writes the column of acc selected by rs1 from vd in the floating-point format selected by SEW using the length specified by TR. This transfer may involve some format conversion to the internal accumulator format from the specified floating-point format.
- vrwaccr rs1, vs2 writes the raw format row of acc selected by rs1 from vs2 as bytes as determined by acccolb.
- vmacc.avx vs1, rs2 performs an integer outer product vector-scalar multiply/accumulate (acc ← acc + vs1 × rs2) for the current settings of SEW and VL. This supports 4× widening for SEW=8. Only the rows of accumulators required to accommodate VL elements are modified.
- vfmacc.avf vs1, fs2 performs a floating-pointer outer product vector-scalar multiply/accumulate (acc ← acc + vs1 × fs2) for the current settings of SEW and VL. This supports 4× widening for SEW=8. Only the rows of accumulators required to accommodate VL elements are modified.

It may be appropriate to specify the width of accumulators as exactly 32 bits each. Any accumulation to int64 or FP32 would use pairs of accumulators. In this case the number of accumulators would be accrows × (acccolb / 4). This proposal recommends sizing accumulator array to V×V to match the load bandwidth for the minimum SEW supported (i.e. MLEN/SEWmin), or to 2V×2V to double element reuse and halve the energy associated with DRAM reads, but implementations might choose smaller accumulator arrays to save area, or yet larger ones for even greater energy savings. Such microarchitectural flexibility is an explicit goal of this proposal.

Extra Accumulators

Accumulators are cheap enough when integrated into the multiply/add array that the question should be not be how to eliminate them, but whether it makes sense to quadruple the number. This would allow $C$ tiles of $2 V \times 2 V$ and thus twice the element reuse and energy savings that results. To simply obtain energy savings, vectors of $2 V$ elements would be loaded from $A$ and $B$ and the multiply/add array would be used eight times (instead of twice) to accumulate the $4 V^{2}$ outer product. This requires eight accumulators per multiply/add units. The computation is no longer balanced, as the loads take four cycles and computation eight cycles. This further has the advantage of naturally matching the Δ=4 case. Balance can be restored by doubling the number of multiply/add units, to achieve four cycles rather than eight, and Δ=4 is still naturally handled. The disadvantage of taking the outer product of $2 V$ elements rather than $V$ elements is simply the 4× storage required for the accumulator array. The advantages of the bigger outer product are enumerated below:

Twice the element reuse and thus half the number of memory accesses to $A$ and $B$ , resulting in almost twice the energy efficiency.
The option to employ twice as many multiply/add units and thus halve the computation time exists (the difference between the 8-cycle and 4-cycle options).
The outer product becomes a 4 or 8-cycle operation, giving more time for address arithmetic and loop overhead.
The Δ=4 case is handled naturally and is no longer a special case.

Below the Load Bandwidth Limit

Some implementations may choose to use a smaller multiply/add array than what is required to reach the load bandwidth limit due to area constraints, i.e. choose a multiply/add array smaller than $V \times (V / 2)$ for $Δ \leq 2$ or $2 V \times (V / 2)$ for $Δ = 4$ . In this case, the outer product method would typically still load $V$ elements from each of $A$ and $B$ . There are two options once the vectors are loaded. The first option maintains a V×V tile size and thus $V^{2}$ accumulators and iterates the implementation’s multiply/add array multiple times to compute this tile. The second option reduces the tile size to reduce the number of accumulators, and instead uses the extra loaded elements as if they were loaded on subsequent iterations for the smaller tile. For the first option, the outerproduct instruction takes more cycles. For the second option, smaller tiles result in (V/T)² times as many tile computations.

Full Accumulator Array Reduced Multipliers

The first option is appropriate when $V^{2}$ accumulators are possible, but the multiply/add units are limited. In this case, $T = V$ , and the $M R \times M C$ multiply/add array is used $(V / M R) \times (V / M C)$ times on all combinations from the two vectors into a $V \times V$ tile of $C$ . This option reduces the number of times source data from $A$ and $B$ has to be loaded. Each element is used $V$ times rather than only the $T$ times of the first option.

The LBMA column is the number of multiply/add units required to match the load bandwidth. The MA column is the number provided by a sub-bandwidth implementation, possibly organized as indicated in the array column. The Cycles Ld gives the cycles to load the vectors, and the Cycles MA gives the cycles to use the array to compute the tile. The Rel column gives the cycle multiple of the overall computation relative to the full array case, and is equal to the LBMA/MA ratio and also equal to the CyclesMA/CyclesLd ratio.

Example sub-bandwidth full accumulators (T=V) for 512 load bits per cycle
Type			Δ	V	LBMA	MA	C tile	array	Cycles		Rel
C	A	B	Δ	V	LBMA	MA	C tile	array	Ld	MA	Rel
int32	int8	int8	1	64	2048	2048	64×64	64×32	2	2	1
						1024		32×32	2	4	2
						512		32×16	2	8	4
						256		16×16	2	16	8
						128		16×8	2	32	16
TF32	BF16	BF16	2	32	512	512	32×32	32×16	2	2	1
						256		32×8	2	4	2
						128		16×8	2	8	4
FP32	BF16	BF16	4	32	512	512	64×64	32×16	4	16	1
						512	2×32×32	32×16	4	4	1
						256	32×32	32×8	2	4	2
						128		16×8	2	8	4
						64		8×8	2	16	8
FP32	FP32	FP32	4	16	128	128	32×32	16×8	4	16	1
						128	2×16×16	16×8	4	4	1
						64	16×16	16×4	2	4	2

Reduced Accumulator and Multiplier Arrays

The second option is appropriate when both accumulator storage and multiply/add units are limited and so targets $T^{2}$ accumulators ( $T < V$ ) representing a $T \times T$ tile of $C$ by iterating $V / T$ times to accumulate the outer product of $T$ element portions of the loaded vectors using a multiply/add array of $T \times (T / Δ)$ . Consider some example cases in the table below.

The LBMA column is the number of multiply/add units required to match the load bandwidth. The MA column is the number provided by a sub-bandwidth implementation, possibly organized as indicated in the array column. The Tile ratio column gives the multiplier on the number of tiles that must be computed. The V/T column specifies the how many outer products are add to the C tile. The Cycles Ld gives the cycles to load the vectors, and the Cycles MA gives the cycles to use the array to compute the tile. The Rel column gives the cycle multiple of the overall computation relative to the full array case, and is equal to the LBMA/MA ratio.

Example sub-bandwidth reduced accumulators for 512 load bits per cycle
Type			Δ	V	LBMA	MA	C tile	Tile	Use	array	V/T	Cycles		Rel
C	A	B	Δ	V	LBMA	MA	C tile	ratio		array	V/T	Ld	MA	Rel
int32	int8	int8	1	64	2048	2048	64×64	1	1	64×32	1	2	2	1
						1024	64×64	1	1	32×32	1	2	4	2
						1024	32×32	4	½	32×32	2	2	2	2
						512	32×32	4	½	32×16	2	2	4	4
						256	16×16	16	¼	16×16	4	2	4	8
						128	16×16	16	¼	16×8	4	2	8	16
TF32	BF16	BF16	2	32	512	512	32×32	1	1	32×16	1	2	2	1
						256	32×32	1	1	32×8	1	2	4	2
						128	16×16	4	½	16×8	2	2	8	4
FP32	BF16	BF16	4	32	512	512	64×64	¼	2	32×16	½	4	4	1
						512	2×32×32	2	1	32×16	1	4	4	1
						256	32×32	1	1	32×8	1	2	4	2
						128	16×16	4	½	16×8	2	2	8	4
						64	16×16	4	½	16×4	2	2	16	8
FP32	FP32	FP32	4	16	128	128	2×16×16	2	1	16×8	1	4	4	1
FP32	FP32	FP32	4	16	128	64	16×16	1	1	16×4	1	2	4	2

Open Issues

The accumulation formats for all values of SEW and integer and floating-point need to be nailed down. For example, is TF32 used for some accumulation? How many guard bits are required for integer accumulation, and are there any fixed point shifts?

How should BF16 be accommodated? How should the three IEEE 754 binary8p* formats be accommodated?

Does the acc internal representation need to be specified for migration from one RISC‑V implementation to another?

Other Methods

How does the outer product method compare to other methods for matrix multiply? To that end, we need to explore those methods a bit. The following subsections do that.

Avoiding Accumulators

Other proposals for RISC‑V matrix extensions propose storing matrixes in the Vector Register File (VRF). For example, storing $C$ , $A$ , and $B$ in the VRF and adding a matrix multiply instruction that does vd ← vd + matmul(vs1, vs2). (This is likely implemented by using local accumulators internally with transfers to/from vd to the local accumulators.) The problem is the size of the matrixes that can be accommodated by the VRF limits the performance of this approach. With LMUL=8, there are only 4 vector registers (v0, v8, v16, v24) available for use, which might be enough given 3 matrixes, but which might be limiting for scheduling purposes. LMUL=4 is a safer assumption, since that provides 8 vector registers (v0, v4, …, v28).

Working an example again might illustrate the issues. To match the outer product performance, consider using 32×32 tiles of 16‑bit elements, making each matrix operand 16384 bits (for LMUL=4 this requires VLEN≥4096), making the VRF at least 131072 bits, which is large compared to what is required for the outer product method, and which also does not include the internal array state that is probably appropriate. The minimum cycle count for this operation is $32 Δ$ , for 32³ multiply/adds, or $1024 / Δ$ multiply/adds per cycle. The instruction needs to first fill internal state from vd (this might take 32 cycles), perform $32 Δ$ cycles of computation, and then transfer the internal state back to vd (another 32 cycles). The fill and unfill would be pipelined so another tile multiply could start every $32 Δ$ cycles. In addition, 32768 bits would be loaded from memory every 32L cycles (1024 bits per Δ cycles) to keep the tile multiply instructions supplied with data. The problems with this approach include the long cycle count (perhaps 128 cycles), the state machines to sequence the operations, the power wasted transferring to and from vd, and the size of the VRF coupled with VRF entries requiring a minimum of 4 read ports and 2 write ports (and potentially increased in size for renaming). Some power might be saved by noting that the current read of vd would be identical to what was just written from the internal array state, and then skipping writing the same data back to the internal state. Loading, storing, and operating on matrixes has not provided any performance improvement (it remains limited by the load bandwidth), but it has resulted in greater area, poorer energy efficiency, and greater complexity.

A better way to avoid accumulators would be to use software to perform T outer product instructions, targeting accumulation in the Vector Register File (VRF). Again using 32×32 tiles of 16‑bit elements, software would load 512 bits from $A$ , 512 bits from $B$ , compute an outer product in a single instruction that accumulates this in the tile stored in vd, repeatable every two cycles. Perhaps LMUL=8 is reasonable in this case. Only the accumulation tile is 16384 bits, which for LMUL=8 requires VLEN≥2048, leaving the VRF a less gargantuan 65536 bits. The computation is similar to the outer product instruction to local accumulators, except that transfers into and out of the computation array are necessary, costing considerable time and energy. To solve this problem, add back the internal array state, and upon noticing that the current read of vd would be identical to what was just written from the internal array state, skipping writing the same data back to the internal state. Once again, this option has not provided any performance improvement (it remains limited by the load bandwidth), but it has resulted in greater area, poorer energy efficiency, and greater complexity. The only savings is to avoid extra state to be context switched by the supervisor.

Matrixes in the Vector Register File

Other proposals for RISC‑V matrix extensions propose storing tiles in a Matrix Register File (MRF), either by adding a separate MRF, or mapping the MRF to the existing Vector Register File (VRF).

To keep the math simpler, we analyze only the fully square case $m = n = p = T$ and the rectangular case $m = 2 T, n = p = T$ . The computational intensity of the square case is $T^{3}$ multiply/adds for $2 T^{2}$ elements loaded, for a computational intensity of $T / 2$ . This is identical to the computational intensity of the outer product method. The computational intensity of the rectangular tile is $2 T^{3}$ multiply/adds for $3 T^{2}$ elements loaded, for a computational intensity of $2 T / 3$ .

Similarly, for the fully square case is $T^{3}$ multiply/adds for $3 T^{2}$ elements stored in registers which is considerably larger than the vector and outer product accumulator methods.

When the Vector Register File (VRF) is used to store matrixes rather than vectors, the first case is when the VRF size remains the same. Microarchitectures have significant flexibility in choosing the VRF parameters such as VLEN (the VRF size is VLEN×32 bits), so to analyze this case, it is necessary to look at the considerations that typically influence VRF size. Some of these are enumerated below.

The performance target for the algorithms to be executed by the vector unit provides a lower bound for the width of the datapath (herein called DLEN) containing the VRF and execution units.
The degree of instruction level parallelism (e.g. the width of instruction issue and whether in-order or out-of-order) influences VLEN via the number of cycles it takes from one load, store, or op to the next. Vector units should be able to operate in parallel with the instructions that are setting up the next vector operation to the same unit. By setting up the next unit operation and then waiting for the unit to complete, the unit is not left idle. A processor with a high Instructions Per Cycle (IPC) can tolerate VLEN = DLEN (which is essentially SIMD rather than vector). High IPC processors typically employ Out-of-Order (OoO) hardware scheduling and register renaming, and register renaming makes VRF bits more expensive, putting pressure for VLEN = DLEN. Lower IPC processors need VLEN > DLEN to be effective.
The width of the datapath DLEN influences VLEN as the ratio VLEN×LMUL/DLEN determines the how many cycles units in the datapath will operate.
Often the load/store bandwidth (herein called MLEN) is the same as DLEN. When it is different from DLEN, it may also influences the choice of VLEN by making loads operate for VLEN×LMUL/MLEN cycles in parallel with the instructions setting up the next vector load or store. Typically MLEN = DLEN or MLEN = 2×DLEN. Elsewhere this document refers to the load bandwidth, V, in elements, which is V = MLEN/SEW for the element width under consideration.
The LMUL setting for the algorithms most important for the vector unit to execute well, due to its effect on cycles that units operate before needing additional setup as described above.

Given the above, it is expected that many high-IPC microarchitectures will choose VLEN = MLEN and the analysis will be based on VRFbits=MLEN×32. Conversely, many low-IPC microarchitectures will have VLEN = MLEN×2 for targeting LMUL=2 algorithms or VLEN = MLEN×4 targeting LMUL=1 algorithms, since in both cases there are four cycles to setup the next vector operation to a unit (e.g. multiply/add, load/store), which allows modest instruction level parallelism to accomplish in 6-8 instructions (including loop iteration). Some low-IPC microarchitectures might choose another factor of two, but the analysis here will use VRFbits=MLEN×64 when LMUL=2 algorithms are the primary target, and VRFbits=MLEN×128 when LMUL=1 algorithms are significant. Since this analysis is often based on the VRF size, denoted W, and load bandwidth V, both expressed in elements of EEW bits, then $W = 64 V$ or $W = 128 V$ . For the high-IPC case, $W = 32 V$ may be appropriate.

For a processor with $W = 64 V$ , the VRF can hold three (one wide) square matrixes with $T = \sqrt{W / 4} = \sqrt{16 V} = 4 \sqrt{V}$ . For even powers of two, this is exact (i.e., $V = 2^{2 n}$ suggests $T = 2^{n + 2}$ ), and for odd powers of two, either square tiles with $T = 2^{n + 2}$ or rectangular tiles, $T \times 2 T$ may be used (i.e., for $V = 2^{2 n + 1}$ , the tile is $2^{n + 2} \times 2^{n + 3}$ ). The following analysis will first consider $C$ , $A$ , and $B$ all being $T \times T$ . A second analysis for $C$ being $T \times 2 T$ , $A$ being $T \times T$ , and $B$ being $T \times 2 T$ is considered. The reader is invited to generalize the dimensions of $A$ to $T \times X$ , and therefore the dimensions of $B$ to $X \times T$ or $X \times 2 T$ for the two cases.

The product of two $T \times T$ matrixes can be done in $T Δ$ cycles using $T^{2} / Δ$ pipelined multiply/add units, and the loads of the two source matrixes require $2 T^{2} / V$ cycles. Loads and computation are balanced when $T = V Δ / 2$ . The computation rate is $T^{2} / Δ$ when $T \leq V Δ / 2$ , and $T V / 2$ when $T \geq V Δ / 2$ . For the suggested $T = 4 \sqrt{V}$ . the computation is load limited when $V < 64 / Δ^{2}$ .

When $C$ is $T \times 2 T$ $A$ will be $T \times X$ and $B$ will be $X \times 2 T$ , where generally $X = T$ , in which case the product can also be done in $T Δ$ cycles but in this case using $2 T^{2}$ multipliers. The loads of the two source matrixes require $3 T^{2} / V$ cycles. Loads and computation are balanced when $T = V Δ / 3$ . The computation rate is $2 T^{2} / Δ$ when $T \leq V Δ / 3$ , and $⅔ T V$ when $T \geq V Δ / 3$ . The rectangular case doubles the computation rate unless load bandwidth limited, in which case the computation rate increases by only 50%.

The reader is invited to repeat the above analysis for $W = 128 V$ (the case when LMUL=1 algorithms are the primary target on low-IPC processors) and for $W = 32 V$ for high-IPC processors.

For example, given VLEN=1024, MLEN=512, SEW=16, then V=32, W=2048, and T=22. Rounding down to a power of two, matrixes of 16×16 or 16×32 would be stored, with four rows stored in four 1024-bit vector registers. The loading of two 16×16 matrixes takes 16 cycles and the computation takes 16×Δ cycles, and so this implementation is leaving the load bandwidth highly underutilized unless Δ=1. The computation rate is 16³/(16×Δ) = 256/Δ multiply/adds per cycle. For comparison, given the same parameters, 32 iterations of the outer product with tile accumulation would use two registers for loads of 32 elements, taking 64 cycles and then an outer product into a 32² = 1024 element accumulator array, taking 32×Δ cycles. This is balanced for Δ=2. The computation rate is 32³/(32×Δ) = 1024/Δ multiply/adds per cycle, or four times the rate of doing matrix-matrix products. Note however, that 1024 element accumulation matrix with widening requires the entire VRF in this case, leaving no space for loading the vectors for the outer product. This suggests that the accumulator array should be separate from the VRF for both size and energy efficiency reasons.

An enumeration of choices of VRF parameters and the resulting matrixes that can be stored for various SEW and EEW is given in a separate page Table Comparison of Matrixes in Vector Register File with Outer Product Accumulators, which is meant to be viewed/printed in landscape mode. This table also includes the Outer Product Array (OPA) performance for comparison. As can be seen in the table, the advantage of outer product over matrixes in the VRF increases with DLEN/MLEN/VLEN.

Inner Product Methods

SiFive’s Inner-Product Matrix Extensions proposal to the RISC‑V IME TG is another method based on specialized parallel inner product hardware for two extensions. Xsfvmm32a8i adds sf.vqmmacc*.vv for int32 ← int32 + int8 × int8. Xsfvmm32a16f adds sf.vfwmmacc.vv for fp32 ← fp32 + fp16 × fp16. and sf.vfwmmacc.bf.vv for fp32 ← fp32 + bf16 × bf16. Using LMUL=1 (i.e. VL≤VLEN/SEW), it accumulates to a 23×8 tile of C, held in 23 vector registers, the product of a 23×VL tile of A and a VL×8 tile of B, held in 8 vector registers. The core multiply/add instructions compute the matrix-vector product $𝒄 \leftarrow 𝒄 + 𝒂 B$ where $𝒄$ is 1×8, $𝒂$ is 1×VL, and $B$ is VL×8. These instructions are used 23 times to compute the product of the A and B tiles. As a refresher, for the general matrix/tile multiply where C is m×p, A is m×n, and B is n×p, the number of multiply/adds is $m n p$ and the latency for a maximally parallel implementation usually has latency $n Δ$ using $m p / Δ$ multiply/adds. (As a reminder Δ is the number of cycles between dependent adds.) What is typically done to maximize parallelism is to maximize the tile $m$ and $p$ . It is unusual to maximize the tile $n$ in matrix multiplication, since that maximizes the latency. For example, the fully-parallel outer product can be thought of minimizing $n$ by picking $n = 1$ . The latency of inner products increases linearly with VL. This approach is only advantageous when $Δ < 1$ , and especially when $Δ ≪ 1$ , which is possible when carry-save arithmetic is used for the summation, for example, by using a log tree of 3:2 compressors followed by a single carry-propagate add. This works naturally for integer summation; for floating-point block normalization can be used, aligning all the values to be summed to the largest exponent, followed by integer arithmetic to calculate the sum, which is then normalized and rounded.

The choice of 8 and 23 is based on Vector Register File (VRF) considerations. Since some data formats require quad-widening (e.g. int32 ← int32 + int8 × int8) and LMUL=1, the minimum VLEN for this extension, 256, fits eight 32‑bit values. This determines the number of columns of the accumulation and the number of vector registers to hold the B tile. One vector register is required to load rows of the A tile. This leaves 23 vector registers for the C tile accumulation.

The pseudo-code for this proposal is given below:

    for ti ← 0 to m-1 step 23
      for tj ← 0 to n-1 step 8
	// load 23×8 C tile
        v8 ← c[ti+ 0,tj..tj+7]
        v9 ← c[ti+ 1,tj..tj+7]
	⋮
	v30 ← c[ti+22,tj..tj+7]
	for tk ← 0 to n-1 step VL
	  // load 8×VL B tile
	  v0 ← b[tk..tk+VL-1,tj+0]
	  v1 ← b[tk..tk+VL-1,tj+1]
	  v2 ← b[tk..tk+VL-1,tj+2]
	  v3 ← b[tk..tk+VL-1,tj+3]
	  v4 ← b[tk..tk+VL-1,tj+4]
	  v5 ← b[tk..tk+VL-1,tj+5]
	  v6 ← b[tk..tk+VL-1,tj+6]
	  v7 ← b[tk..tk+VL-1,tj+7]
	  // unrolled operations on rows of A and C
	  v31 ← a[ti+0,tk..tk+VL-1]		// vle to load row of A
	  v8 ← sf.vqmmacc.vv(v8, v31, v0..v7, 0)	// 10R1W matrix×vector
	  v31 ← a[ti+1,tk..tk+VL-1]		// vle to load row of A
	  v9 ← sf.vqmmacc.vv(v9, v31, v0..v7, 0)	// 10R1W matrix×vector
	  ⋮
	  v31 ← a[ti+23,tk..tk+VL-1]		// vle to load row of A
	  v30 ← sf.vqmmacc.vv(v30, v31, v0..v7, 0)// 10R1W matrix×vector
	// write back 23×8 C tile
        c[ti+ 0,tj..tj+7] ← v8
        c[ti+ 1,tj..tj+7] ← v9
	⋮
	c[ti+22,tj..tj+7] ← v30

The inner loop has:

31 vector loads (VLEN bits each), each taking VLEN/MLEN cycles;
23 sf.*, each taking VLEN/DLEN cycles;
and 37 integer instructions (31 address adds associated with loads and 6 others).

This is a total of 91 instructions. The number of multiply/adds is 23×8×VL=184×VL. The Computational Intensity (CI) is 184×VL / (31×VL) = 5.935.

When VLEN > 256, another tiling is possible, accumulating to a 15×16 tile of C, held in 15 vector registers, the product of a 15×VL tile of A and a VL×16 tile of B, held in 16 vector registers. The same matrix-vector product accumulation instructions are used twice, with different offsets into the accumulation vector register. is VL×16. These instruction pairs are used 15 times to compute the product of the A and B tiles. The number of multiply/adds is 15×16×VL=240×VL. The Computational Intensity (CI) is 240×VL / (31×VL) = 7.742.

    for ti ← 0 to m-1 step 15
      for tj ← 0 to n-1 step 16
	// load 15×16 C tile
        v16 ← c[ti+ 0,tj..tj+15]				// load C tile into
        v17 ← c[ti+ 1,tj..tj+15]				// 15 vector registers
	⋮							// holding 16 elements each
	v30 ← c[ti+14,tj..tj+15]
	for tk ← 0 to n-1 step VL
	  // load 16×VL B tile
	  v0 ← b[tk..tk+VL-1,tj+0]
	  v1 ← b[tk..tk+VL-1,tj+1]
	  ⋮
	  v15 ← b[tk..tk+VL-1,tj+15]
	  // unrolled operations on rows of A and C
	  v31 ← a[ti+0,tk..tk+VL-1]			// vle to load row of A
	  v16 ← sf.vqmmacc.vv(v16, v31,  v0.. v7, 0)	// 10R1W matrix×vector
	  v16 ← sf.vqmmacc.vv(v16, v31,  v8..v15, 1)	// 10R1W matrix×vector
	  v31 ← a[ti+1,tk..tk+VL-1]			// vle to load row of A
	  v17 ← sf.vqmmacc.vv(v17, v31,  v0.. v7, 0)	// 10R1W matrix×vector
	  v17 ← sf.vqmmacc.vv(v17, v31,  v8..v15, 1)	// 10R1W matrix×vector
	  ⋮
	  v31 ← a[ti+14,tk..tk+VL-1]			// vle to load row of A
	  v30 ← sf.vqmmacc.vv(v30, v31,  v0.. v7, 0)	// 10R1W matrix×vector
	  v30 ← sf.vqmmacc.vv(v30, v31,  v8..v15, 1)	// 10R1W matrix×vector
	// write back 15×16 C tile
        c[ti+ 0,tj..tj+15] ← v16
        c[ti+ 1,tj..tj+15] ← v17
	⋮
	c[ti+14,tj..tj+15] ← v30

The inner loop has:

31 vector loads (VLEN bits each), each taking VLEN/MLEN cycles;
30 sf.*, each taking VLEN/DLEN cycles;
and 37 integer instructions (31 address adds associated with loads and 6 others).

This is a total of 98 instructions. The number of multiply/adds is 15×16×VL=240×VL. The Computational Intensity (CI) is 240×VL / (31×VL) = 7.742.

This document henceforth uses Matrix Vector Accumulator (MVA) as the name for the class of extensions that includes Xsfvmm32a8i and Xsfvmm32a16f. We first compare MVA to RISC‑V Vector (RVV) and then to Outer Product Accumulator (OPA) below. We begin the analysis by enumerating the MVA configurations that make sense based on the VLEN/DLEN ratio and IPC.

When VLEN = DLEN×4, the vector loads and matrix-vector product instructions take 4 cycles each, making the loop 124 cycles based on the vector loads, with the 55 other instructions instructions executing in the shadow of the vector loads. Such configurations work for processors supporting IPC≥1. The 18 VRF reads can be accomplished using two even/odd pair ports over four cycles for the B tile, and two non-pair read ports. The multiply/add rate is then 240×VL/124 = 1.935×VL = 7.7×DLEN/SEW for VLEN = DLEN×4. Since typical RISC‑V Vector achieves a DLEN/SEW rate, this extension is potentially 7.7× more throughput.

When VLEN = DLEN×2, the vector loads and matrix-vector product instructions take 2 cycles each, making the loop 62 cycles based on the vector loads, with the 55 other instructions executing in the shadow of the vector loads. Such configurations work for processors supporting IPC≥2. The 18 VRF reads can be accomplished using four even/odd pair ports over two cycles for the B tile, and two non-pair read ports. The multiply/add rate is then 240×VL/62 = 3.871×VL = 7.7×DLEN/SEW for VLEN = DLEN×2. Thus this configuration is also potentially 7.7× more throughput than RISC‑V Vector, but requires more instructions per cycle and VRF read bandwidth.

When VLEN = DLEN, the vector loads and matrix-vector product instructions take 1 cycle each, making the loop 31 cycles based on the vector loads, with the 55 other instructions executing in the shadow of the vector loads. Such configurations work for processors supporting IPC≥3. The 10 VRF reads can be accomplished using four even/odd pair ports for the B tile, and two non-pair read ports. The multiply/add rate is then 184×VL/31 = 5.9×VL = 5.9×DLEN/SEW for VLEN = DLEN. Thus this configuration is also potentially 5.9× more throughput than RISC‑V Vector, but requires still more instructions per cycle and VRF read bandwidth.

For energy efficiency loads from the L2 cache are an important component. For VLEN = 256, each element loaded from the A tile is used 8 times and each element loaded from the B tile is used 23 times. For example, for 16‑bit data, a 256 KiB L2 cache fitting 256×256 A and B tiles, the L2 is referenced 256/8=32 times for A and ⌈256/23⌉=12 times for B (total 44). Compared to RISC‑V Vector (RVV), MVA is sometimes requires fewer L2 reads (less energy) and sometimes more L2 reads (more energy). Since RVV does not support quad-widening, so a sf.vqmmacc.vv comparison with SEW=8 EEW=32 is not possible, consider comparing sf.vfwmmacc.bf.vv to the RVV configuration DLEN=256, VLEN=512, SEW=16, EEW=32, LMUL=2: the C tile would be 8×32, A would be scalar loads each used 32 times, and B would be a 32-element vector loads used 8 times, and the L2 referenced 256/32=8 times for A and 256/8=32 for B (total 40), making MVA 1.1× the L2 references of RVV. There is a savings is VRF reads: this method requires 1.25 register reads per multiply/add, compared to 2-3 per multiply/add for RVV. VRF writes are 0.29 and 1.1 for inner product vs. RVV, respectively. There are also configurations where the inner product method reduces the L2 references; see the table cited below.

For VLEN > 256, each element loaded from the A tile is used 16 times and each element loaded from the B tile is used 15 times. For example, for 16‑bit data, a 256 KiB L2 cache fitting 256×256 A and B tiles, the L2 is referenced 256/16=16 times for A and ⌈256/15⌉=18 times for B (total 34).

When compared to Outer Product Accumulators (OPA), sf.vfwmmacc.bf.vv is generally less performance and more energy. Using the same configuration as above, OPA would accumulate the outer product of 16‑element A and B vectors into a 16×16 array of 32‑bit accumulators in the 16×8 multiply/add array. Each element of A and B would be used 16 times, so the L2 reads would be 256/16=16 for A and B. The 44 reads for MVA is 1.4× the 32 reads for OPA (i.e. 40% more energy for L2 access). For 16‑bit data MVA performs 95 multiply/adds per cycle, and OPA performs 128 multiply/adds per cycle, or 1.35× the throughput. The disparity widens as DLEN and VLEN increase; for DLEN=512, VLEN=1024, OPA performs 512 multiply/adds per cycle compared to 190 for MVA, a factor of 2.7×, while MVA requires 2.8× as many L2 accesses. Since MVA and OPA both support quad-widening, it is worth comparing sf.vqmmacc.vv to OPA for this second configuration: MVA is 380 multiply/adds per cycle compared to 2048 for OPA, a factor 10.8×. In addition, MVA makes 11.0× the number of L2 access as OPA.

Since the comparative throughput and L2 accesses of RVV, MVA, and OPA depend quite a bit by IPC, DLEN, VLEN, SEW, and EEW, the separate Table Comparison of Matrix Vector Product Accumulation with Outer Product Accumulation may be useful (landscape mode or a wide screen is necessary for viewing). This table is meant to be representative of what would typically be done; not all possible design choices are incorporated in the table. Below are a few of the lines of that table for SEW=8 EEW=32 IPC=2 and IPC=3. The RVV columns from the table cited above are omitted below because RVV does not support quad-widening (required for the EEW/SEW ratio chosen for sampling). This also keeps the table width consistent with this document.

The Computation Intensity (CI) of MVA is either 5.935 for 8×23 or 7.742 for 16×15. The CI of OPA is $½ T$ .

Comparison of Matrix-Vector Product with Outer Product Accumulators for SEW=8 EEW=32 Δ=1
Base	VRF				MVA						OPA
IPC	DLEN bits	VLEN bits	VRF bytes	pair ports	m	n	p	loop cyc	MAC /cyc	CI	acc	acc bytes	MAC /cyc	CI	MVA ratio	load ratio
2	256	256	1024	1	23	8	32	92	64	5.9	32×32	4096	512	16	8.0×	2.8×
2	256	256	1024	2	23	8	32	46	128	5.9	32×32	4096	512	16	4.0×	2.8×
2	256	256	1024	4	23	8	32	46	128	5.9	32×32	4096	512	16	4.0×	2.8×
2	256	512	2048	1	23	8	64	92	128	5.9	32×32	4096	512	16	4.0×	2.8×
2	256	512	2048	1	15	16	64	120	128	7.7	32×32	4096	512	16	4.0×	2.1×
2	256	512	2048	2	23	8	64	62	190	5.9	32×32	4096	512	16	2.7×	2.8×
2	256	512	2048	2	15	16	64	62	248	7.7	32×32	4096	512	16	2.1×	2.1×
2	256	512	2048	4	23	8	64	62	190	5.9	32×32	4096	512	16	2.7×	2.8×
2	256	512	2048	4	15	16	64	62	248	7.7	32×32	4096	512	16	2.1×	2.1×
2	512	512	2048	1	23	8	64	92	128	5.9	64×64	16384	2048	32	16.0×	5.5×
2	512	512	2048	1	15	16	64	120	128	7.7	64×64	16384	2048	32	16.0×	4.2×
2	512	512	2048	2	23	8	64	46	256	5.9	64×64	16384	2048	32	8.0×	5.5×
2	512	512	2048	2	15	16	64	60	256	7.7	64×64	16384	2048	32	8.0×	4.2×
2	512	512	2048	4	23	8	64	46	256	5.9	64×64	16384	2048	32	8.0×	5.5×
2	512	512	2048	4	15	16	64	49	313	7.7	64×64	16384	2048	32	6.5×	4.2×
2	512	1024	4096	1	23	8	128	92	256	5.9	64×64	16384	2048	32	8.0×	5.5×
2	512	1024	4096	1	15	16	128	120	256	7.7	64×64	16384	2048	32	8.0×	4.2×
2	512	1024	4096	2	23	8	128	62	380	5.9	64×64	16384	2048	32	5.4×	5.5×
2	512	1024	4096	2	15	16	128	62	495	7.7	64×64	16384	2048	32	4.1×	4.2×
2	512	1024	4096	4	23	8	128	62	380	5.9	64×64	16384	2048	32	5.4×	5.5×
2	512	1024	4096	4	15	16	128	62	495	7.7	64×64	16384	2048	32	4.1×	4.2×
Base	VRF				MVA						OPA
IPC	DLEN bits	VLEN bits	VRF bytes	pair ports	m	n	p	loop cyc	MAC /cyc	CI	acc	acc bytes	MAC /cyc	CI	MVA ratio	load ratio
3	256	256	1024	1	23	8	32	92	64	5.9	32×32	4096	512	16	8.0×	2.8×
3	256	256	1024	2	23	8	32	46	128	5.9	32×32	4096	512	16	4.0×	2.8×
3	256	256	1024	4	23	8	32	31	190	5.9	32×32	4096	512	16	2.7×	2.8×
3	256	512	2048	1	23	8	64	92	128	5.9	32×32	4096	512	16	4.0×	2.8×
3	256	512	2048	1	15	16	64	120	128	7.7	32×32	4096	512	16	4.0×	2.1×
3	256	512	2048	2	23	8	64	62	190	5.9	32×32	4096	512	16	2.7×	2.8×
3	256	512	2048	2	15	16	64	62	248	7.7	32×32	4096	512	16	2.1×	2.1×
3	256	512	2048	4	23	8	64	62	190	5.9	32×32	4096	512	16	2.7×	2.8×
3	256	512	2048	4	15	16	64	62	248	7.7	32×32	4096	512	16	2.1×	2.1×
3	512	512	2048	1	23	8	64	92	128	5.9	64×64	16384	2048	32	16.0×	5.5×
3	512	512	2048	1	15	16	64	120	128	7.7	64×64	16384	2048	32	16.0×	4.2×
3	512	512	2048	2	23	8	64	46	256	5.9	64×64	16384	2048	32	8.0×	5.5×
3	512	512	2048	2	15	16	64	60	256	7.7	64×64	16384	2048	32	8.0×	4.2×
3	512	512	2048	4	23	8	64	31	380	5.9	64×64	16384	2048	32	5.4×	5.5×
3	512	512	2048	4	15	16	64	33	465	7.7	64×64	16384	2048	32	4.4×	4.2×
3	512	1024	4096	1	23	8	128	92	256	5.9	64×64	16384	2048	32	8.0×	5.5×
3	512	1024	4096	1	15	16	128	120	256	7.7	64×64	16384	2048	32	8.0×	4.2×
3	512	1024	4096	2	23	8	128	62	380	5.9	64×64	16384	2048	32	5.4×	5.5×
3	512	1024	4096	2	15	16	128	62	495	7.7	64×64	16384	2048	32	4.1×	4.2×
3	512	1024	4096	4	23	8	128	62	380	5.9	64×64	16384	2048	32	5.4×	5.5×
3	512	1024	4096	4	15	16	128	62	495	7.7	64×64	16384	2048	32	4.1×	4.2×

There are a number of pros and cons to this approach:

	Pros	Cons
RVV	Existing solution typically achieving DLEN/SEW multiply/adds per cycle Well-defined rounding	Does not support quad-widening or octo-widening Scalability limited by 32 Vector Registers
MVA	Supports quad-widening and octo-widening More throughput than RVV for most configurations May extend to mixed-precision support No state addition to RVV Same register renaming requirements as RVV CI = 5.935 for 8×23 CI = 7.742 for 16×15 (VLEN > 256)	Potentially different FP rounding from RVV and between MVA implementations due to inner product latency issues Optimal code sequence depends on VLEN, so runtime dispatch to multiple loops may be required Extra Vector Register File banking required for many configurations (extra ports for a few configurations) Scalability limited by 32 Vector Registers Format-specific sum reduction hardware Generally lower performance and more L2 references than OPA VLEN ≤ 128 not supported
OPA	Supports quad-widening and octo-widening Usually delivers best throughput and energy efficiency Performance and efficiency increase quadratically with DLEN Accumulator bits are much less expensive than Vector Register File bits Easily scalable up by increasing accumulator array size and LMUL without change to VRF Easily scalable down by decreasing accumulator array size without change to VRF Possible to match compute to load bandwidth Potentially well-defined rounding VLEN ≤ 128 supported Provides efficient transpose in addition to matrix multiplication	Accumulators are extra state, potentially large OoO processors either need to rename accumulators or perform outer product accumulation after commit

Comparison of Methods

Square tiles are generally the best choice, except perhaps for vector where the number of vector registers limits tiles to 16×16 for EMUL≤1 and to 8×8 for EMUL=2. Thus the table below uses square tiles for the Outer Product Array (OPA) and Matrix Register File (MRF) methods below. OPA and MRF are split into Δ≤2 and Δ=4 cases as described in the Matrix Multiply Using An Outer Product Array section above. Δ=3 and Δ≥5 are not considered.

The Acc column gives where tiles are accumulated. The LBM column gives whether Load Bandwidth Matching is feasible (generally not for Vector unless the load elements per cycle is small). The C column gives the number of multiply/add computations per inner loop. The Load column gives the number of elements loaded per inner loop. The CI column gives the Computation Intensity (CI), or C/Load. Loading of accumulation tile is not included in Computational Intensity (CI) because that is negligible for large matrixes, being outside of the k loop. The Register Requirement in elements for matching the load bandwidth limit is given in column RR, except for the vector methods where matching is generally not feasible. The number of multiply/add units required to match the load bandwidth $V$ is given in column MAR.

Matrix Multiply Method Comparison
Method	Acc	LBM	C	Load	CI	RR	MAR	Notes
Vector T×T	VRF	$V \leq 2$ only	$T^{2}$	$2 T$	$½ T$	$T^{2} + T + 1$	$T$	Number of vector registers limits $T \leq 30$ . Expect $T = 16$ for EMUL≤1. Expect $T = 8$ for EMUL=2. Usually not feasible to reach load bandwidth limit. RISC‑V requires a scalar register for vector × scalar, hence the $T + 1$ rather than $2 T$ etc. for RR.
Vector T×2T		$V \leq 4$ only	$2 T^{2}$	$3 T$	$⅔ T$	$T^{2} + 2 T + 1$	$2 T$
Vector T×4T		$V \leq 8$ only	$4 T^{2}$	$5 T$	$⅘ T$	$T^{2} + 4 T + 1$	$4 T$
OPA T×T Δ≤2	ACC	$T = V$	$T^{2}$	$2 T$	$½ T$	$T^{2} + 2 T$	$V \times (V / 2)$	ACC storage cheaper than VRF, and lower power. Matching load bandwidth requires $T = V$ .
OPA T×T ×2 Δ=4	ACC	$T = V$ two tiles	$2 T^{2}$	$4 T$	$½ T$	$2 T^{2} + 2 T$	$2 V \times (V / 2)$	ACC storage cheaper than VRF, and lower power. Matching load bandwidth requires two parallel computations with $T = V$ .
MRF T×T Δ≤2	MRF	$T = V$	$T^{3}$	$2 T^{2}$	$½ T$	$3 T^{2}$	$V \times (V / 2)$	Matching load bandwidth requires large MRF with $T = V$ .
MRF T×T ×2 Δ=4	MRF	$T = V$ two tiles	$2 T^{3}$	$4 T^{2}$	$½ T$	$6 T^{2}$	$2 V \times (V / 2)$	Matching load bandwidth requires very large MRF.
MVA 23×8 Δ≪1	VRF	—	$184 VL$	$31 VL$	$5.935$	$32 VL$	—	Generally requires block summation

The comparison finds that vector is limited in its ability to match the load bandwidth. OPA is capable of matching the load bandwidth with minimal VRF usage and a low-power accumulator array, making it superior in all respects to vector. MRF is capable of matching the load bandwidth, but it requires O(V) more register storage in the MRF compared to the OPA VRF requirement, as it requires loading whole matrix tiles before starting an operation, as compared to loading vectors in OPA. The MRF requires up to 3× the bits compared to OPA accumulators because it stores whole A and B tiles, not just the C tile (sometimes less than 3× when the accumulation is in a wider type than the multiplier and multiplicand types). MRF is more complex than OPA (sequencing in hardware rather than software), and likely higher power. OPA is equal or better to MRF in every aspect.

Sizes for load bandwidth matching for 512 bits per cycle
C type	A type	B type	V	Δ	Method	ACC bits	VRF/MRF bits
FP32	FP32	FP32	16	4	OPA	8192	1024
FP32	FP32	FP32	16	4	MRF		24576
FP32	BF16	BF16	32	2	OPA	32768	1024
FP32	BF16	BF16	32	2	MRF		65536
TF32	FP8	FP8	64	2	OPA	77824	1024
TF32	FP8	FP8	64	2	MRF		143360
int32	int8	int8	64	1	OPA	131072	1024
int32	int8	int8	64	1	MRF		196608

Other Operations

This investigation has been primarily about matrix multiplication because O(N³) operations on O(N²) data presents a unique opportunity for performance improvement. Other operations do not present similar O(N) gains. Nonetheless, it is appropriate to at least look at some other operations to see what a matrix extension might include to boost performance less dramatically.

Matrix × Vector

In addition to matrix multiplication, matrix × vector ( $𝒄 \leftarrow 𝒄 + A 𝒙$ ) (where vectors are just $n \times 1$ matrixes) can be important as well. Unfortunately, the existing RISC‑V Vector ISA already captures most of what can be done. If $A$ is an $m \times n$ matrix and $𝒙$ is a column vector (i.e. a $n \times 1$ matrix),

A = (\begin{matrix} a_{1, 1} & a_{1, 2} & \dots & a_{1, n} \\ a_{2, 1} & a_{2, 2} & \dots & a_{2, n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ a_{m, 1} & a_{m, 2} & \dots & a_{m, n} \end{matrix}), 𝒙 = [\begin{matrix} x_{1} \\ x_{2} \\ ⋮ \\ x_{n} \end{matrix}]

then the product $𝒄$ is a $m \times 1$ matrix (i.e. a $m$ -element column vector), such that

𝒄 = [\begin{matrix} c_{1} \\ c_{2} \\ ⋮ \\ c_{m} \end{matrix}] \leftarrow [\begin{matrix} c_{1} + a_{1, 1} x_{1} + a_{1, 2} x_{2} + \dots + a_{1, n} x_{n} \\ c_{2} + a_{2, 1} x_{1} + a_{2, 2} x_{2} + \dots + a_{2, n} x_{n} \\ ⋮ \\ c_{m} + a_{m, 1} x_{1} + a_{m, 2} x_{2} + \dots + a_{m, n} x_{n} \end{matrix}]

Here the amount of source data is $m n + n$ , the number of multiply/adds is $m n$ . The maximum parallelism is $m$ , and the minimum latency is $n Δ$ . The elements of the matrix are each used exactly once; the only load reuse is on vector elements, which are used $m$ times. The parallel computation is the vector scalar products and the sequential computation is the sum, which is seen in the following reformulation:

𝒄 \leftarrow 𝒄 + \sum_{k = 1}^{n} {col}_{k} (A) 𝒙_{k}

For a load bandwidth of $V$ elements per cycle and an add latency of Δ the computation may be pipelined by using $m / Δ$ multiply/add units over $n Δ + Δ - 1$ cycles.

Matrix × Vector using RISC‑V Vector

Matrix vector products are limited by the matrix load bandwidth, as each element is used exactly once. Improving the performance of this operation requires improving the bandwidth of the matrix storage. If the load bandwidth is $V$ elements per cycle, then the RISC‑V vector ISA is sufficient when >2× widening is not required and whenever the vector unit can perform $V$ multiply/adds per cycle and a vector register can hold $V Δ$ elements, which is true of most vector implementations (e.g. by using LMUL≥Δ). The pseudo-code below for matrix × vector calculation without vector reuse is vectorized in the following transformations. The scalar code

  for i ← 0 to m-1
    for j ← 0 to n-1
      c[i] ← c[i] + a[i,j] * x[j]

is converted to use an accumulator:

  for i ← 0 to m-1
    acc ← c[i]
    for j ← 0 to n-1
      acc ← acc + a[i,j] * x[j]
    c[i] ← acc

and then vectorized:

  for i ← 0 to m-1 step VLA
    acc ← c[i..i+VLA-1]
    for j ← 0 to n-1
      acc ← acc + a[i..i+VLA-1,j] * x[j]
    c[i..i+VLA+1] ← acc

The above requires only two vector registers for acc and loading from a. Without widening, RISC‑V allows LMUL=EMUL=8, providing four registers (v0, v8, v16, and v24). This allows VLA to be VLEN*8/SEW. In most vector configurations, it would take at least 8 cycles for loading from a, and one cycle for loading the scalar x[j]. Thus without widening there is sufficient time to satisfy the add recurrence of Δ cycles from one loop iteration to the next for most floating-point implementations (typically Δ≤4). When widening is required, LMUL=4, EMUL=8 would be used, and typically VLA and x[j] would require at least 5 cycles so $Δ \leq 5$ is still non-blocking.

The above exposition did not attempt to achieve any energy savings from vector element reuse. Code to achieve that is shown next. Start from the accumulator version below:

  for i ← 0 to m-1
    acc ← c[i]
    for j ← 0 to n-1
      acc ← acc + a[i,j] * x[j]
    c[i] ← acc

Transform to use reuse x vector loads m times by using a vector register to hold slices of x:

  for tj ← 0 to n-1 step VLX
    vx ← x[tj..tj+VLX-1]
    for i ← 0 to m-1
      acc ← c[i]
      for j ← 0 to VLX-1
        acc ← acc + a[i,tj+j] * vx[j]
      c[i] ← acc

Note that this introduces $n / VLX$ extra loads and stores of c. Note also that this depends on using an indexed element of a vector register as a scalar operand, which is not part of RISC‑V Vector ISA (but could be added). This is then vectorized:

  for tj ← 0 to n-1 step VLX
    vx ← x[tj..tj+VLX-1]
    for i ← 0 to m-1 step VLA
      acc ← c[i..i+VLA-1]
      for j ← 0 to n-1
	acc ← acc + a[i..i+VLA-1,tj+j] * vx[j]
      c[i..i+VLA+1] ← acc

The above requires only three vector registers for vx, acc, and loading from a. Without widening, this allows both VLX and VLA to be VLEN*8/SEW, and therefore vx can hold that number of elements of x for reuse. The matrix loads take VLEN*8/(V*SEW) cycles, which is in most vector configurations is ≥8 cycles. This is sufficient time to satisfy the add recurrence of Δ cycles for most floating-point implementations (typically Δ≤4). When widening is required, LMUL=4, EMUL=8 would be used, and VLEN*4/SEW elements of x are reused and in the typical vector configurations the loads take at least 4 cycles, and so $Δ \leq 4$ is still non-blocking.

The trouble with the above RISC‑V Vector extension is the number of operands required (vd, vs1, vs2, and an rs3 for j). An immediate could be substituted for rs3, but this would require unrolling the loop:

  for tj ← 0 to n-1 step VLX
    vx ← x[tj..tj+VLX-1]
    for i ← 0 to m-1 step VLA
      acc ← c[i..i+VLA-1]
      for j ← 0 to n-1
	acc ← acc + a[i..i+VLA-1,tj+j] * vx[0]
	acc ← acc + a[i..i+VLA-1,tj+j] * vx[1]
	⋮
	acc ← acc + a[i..i+VLA-1,tj+j] * vx[VLX-1]
      c[i..i+VLA+1] ← acc

A second change to RISC‑V Vector would be to allow widening multiply/add with LMUL=8, so EMUL=16 to double the number of elements of x that are used. For example, then v0..v15 could hold acc, v16..v23 could hold x, and v24..v31 could hold the vector loaded from a. This assumes that software pipelining is not required.

Reusing x vector loads only marginally improves the compute intensity; it is primarily done to improve energy efficiency.

To avoid the need for an addition to the RISC‑V vector ISA, it is possible to use the floating-point scalar registers for VLX=32 (or VLX=32*64/SEW—see below). This requires many scalar floating-point loads, or a vector load and transfers to scalar registers, both of which add overhead similar to performing a single scalar load in the inner loop, but there may be microarchitectures where the following is appropriate.

  for tj ← 0 to n-1 step 32
    f0  ← x[tj+ 0]
    f1  ← x[tj+ 1]
    ⋮
    f31 ← x[tj+31]
    for i ← 0 to m-1 step VLA
      acc ← c[i..i+VLA-1]
      acc ← acc + a[i..i+VLA-1,tj+ 0] * f0
      acc ← acc + a[i..i+VLA-1,tj+ 1] * f1
      ⋮
      acc ← acc + a[i..i+VLA-1,tj+31] * f31
      c[i..i+VLA+1] ← acc

For SEW < 64 it would be possible to add a RISC‑V vector extension to pack 64/SEW (2, 4, or 8) values into the f registers by loading with FLD, and then the extension would allow .vf to specify a 3-bit immediate specifying which portion of the f register to use as the scalar operand (and disabling the RISC‑V NaN-boxing check for this packed SIMD reference). This might require a wider vector instruction word. However, if RISC‑V Vector were to be extended, supporting elements from a vector register as scalars would be preferable.

Matrix × Vector using Accumulators

There was one qualification in the previous section, which was that accumulation was non-widening or only used the 2× widening supported by RISC‑V Vector. When ≥4× widening is required, RISC‑V Vector is no longer sufficient. For this case, we turn to the matrix accumulators, which support much wider accumulation than the Vector Register File. We treat the TR×TC accumulators as a vector, rather than as a matrix. This use case is most appropriate when there are Δ times more accumulators than multiply/add units, as occurs naturally for integer (Δ=1), but may be the case for some floating-point configurations. For example, a V×V multiply/add array with four accumulators per multiply/add to implement a 2V×2V accumulation tile for the outer product instructions can support Δ=4 for the matrix vector product. This is illustrated below in pseudo-code (however, the matrix would typically be transposed for unstrided access):

  VL ← min(TR*TC, VLEN/SEW*8)	// limit to LMUL=8 for vector load
  for j ← 0 to m step VL
    acc[0..VL−1] ← y[j..j+VL−1]
    for i ← 0 to n
      v0 ← a[j..j+VL−1,i]	// vector load
      acc ← acc + v0 * x[i]	// vector scalar product in array
    y[j..j+VL−1] ← acc

The additional instructions for the vector scalar product in the array are vmacc.avx vs1, rs2 and vfmacc.avf vs1, fs2.

Batched Matrix × Vector

Batched matrix vector product refers to taking the product of multiple vectors with a given matrix. Batched matrix×vector are just matrix multiplies, and so an outer product array may be used. However, if the batch size is small, it may be that other methods are appropriate. For a batch size p, each matrix element is used p times.

Consideration of batched matrix × vector alternatives to the outer product is TBD. This author thinks such alternatives are unlikely to be helpful, but until further investigation, this is not certain.

Matrix Transpose

Matrix transpose is typically used to rearrange data for efficient stride-1 access and maximize caching and prefetch opportunities. Matrix transpose is typically done by transposing tiles, where the tile size is related to the cache block size. Transpose gets harder as the element size gets smaller. If the cache block size is CB bits and bits per element is SEW, then the best transpose tile size is T×T where T=CB/SEW. This reads T cache blocks from the source and writes the same number of cache blocks transposed at the destination. In between T buffers, each of CB bits, are required, to group the incoming cache blocks into new cache blocks. The total storage requirement is CB²/SEW. As SEW gets small, CB/SEW and CB²/SEW get big, which is the challenge. This storage requirement is related to the storage required for the outer product accumulator array when load and compute are balanced. A typical vector load might load CB bits, i.e. V=CB/SEW. Then a V×V accumulator tile is exactly the right size for transpose. Moreover the wires for writing columns of those accumulators from a row in register file already exist since they are required for the outer product. The basic transpose consists of a loop iterating V times, loading V elements, and writing to one column of accumulators. At the end of the loop the accumulators are filled with the transpose tile, so read them out a row at a time and write as V elements (i.e. a cache block). If the microarchitecture pipelines these operations appropriately, the transpose can operate at the memory limit.

The above is illustrated by the following pseudo-code transformations. First the classic, simple transpose:

  for i ← 0 to n-1
    for j ← 0 to m-1
      c[j,i] = a[i,j]

This is tiled as follows:

  for ti ← 0 to n-1 step T	// tile i
    for tj ← 0 to m-1 step T	// tile j
      // transpose tile from a to c
      for i ← 0 to T-1
        for j ← 0 to T-1
          c[tj+j,ti+i] = a[ti+i,tj+j]

The outer product accumulator array can then be used to perform loads and stores T elements at a time:

  for ti ← 0 to n-1 step T
    for tj ← 0 to m-1 step T
      for i ← 0 to T-1
        va ← a[ti+i,tj..tj+T-1]	// T-element vector load
        acc[0..T-1,i] ← va	// T-element acc write
      for i ← 0 to T-1
	va ← acc[i,0..T-1]	// T-element acc read
        c[tj..tj+T-1] ← va	// T-element vector store

Widening

Widening vector operations are already awkward in RISC‑V Vector, requiring significant complication and cost in the ISA and implementations both, and RISC‑V Vector only supports 2× widening (i.e., EEW=SEW×2). However, there is actually a need for 4× widening, and perhaps even 8×. For example, the product of two 8‑bit integers is 16 bits, and accumulating 4096 of these requires a 28‑bit accumulator. The product of two 4‑bit integers is 8 bits, and accumulating the same number of these products requires 20 bits, which is 5× widening. This is unlikely to be useful when targeting a RISC‑V vector register directly due to the number of cycles it would take.

Once again, an accumulator array can provide a good solution because of the bandwidth and width they provide. If products are accumulated in the matrix accumulators for hundreds or thousands of iterations, and only after exiting the loop are the wide accumulated values written back to a vector register, it is reasonable to provide 4× or 8× widening, and the cycles to write wide results back to vector registers is insignificant. The writing back may also involve a format conversion, reducing the write cycles. For example, accumulation of FP8 (e.g. binary8p5 or binary8p4) data might be done in integer format, and only converted back to a FP8, FP16, or BF16 when read out the accumulators. Accumulation that occurs in FP32 format might similarly be converted to FP16 or BF16 when written to vector registers.

Matrix Addition, Subtraction, Scaling

While it unclear that matrix addition is needed for the applications for which this extension is targeted, should it be required for some other applications, then it is possible to implement multiple accumulators in each computational unit of the two-dimensional array, each capable of holding a $a_{i, j}$ value. The accumulators are then a local register file for each unit. Matrix addition and subtraction, and multiplication (for the Hadamard product ⊙) are then operations between local register file entries. Scaling might be based on a global value from the Vector Register File.

These operations are not useful for computation on matrixes that must be read and written to memory, since those operations are memory bandwidth limited, and so RISC‑V vector has compute equal to the load bandwidth. The primary value of these operations would be for complex matrix expressions, e.g. $A B - C D$ , especially ones that include the result of a matrix multiply and thus a favorable multiply/add to load ratio. Even to do $A B - s D$ , the product tile of $A B$ would be computed from T outer product operations, and the result transferred back to a vector register one row at a time, and a row of $D$ subtracted. Thus matrix operations other than multiply have limited utility, but can be supported when that utility exists.

It is also possible to imagine operations that operate between adjacent rows and columns. For example, one could absolute differences or squared differences between matrixes, then shift a row or a column, for the purposes of doing motion estimation. This would also require some sort of row or column reduction to compute sum of absolute differences.

The addition of such features would take this extension a little bit towards a more general SIMT [wikilink] approach.

Convolution

TBD

Motion Search

TBD

Tiling for the Cache Hierarchy

This proposal has focused on tiling for the datapath execution units, and in particular for an Outer Product Array (OPA). Additional tiling may be appropriate for caches up to and including the Last Level Cache (LLC). For example, a last level tile size of 2048×2048 FP8 values might be used with a LLC of 16 MiB, using about 4 MiB for the A matrix and 4 MiB for the B matrix. The C datapath tiles would also compete for this cache space, but would not particularly benefit from it, since each C datapath tile is read once and written once, whereas for 64×64 datapath tiles, the LLC would source these from A and B 32 times (2048/64) before the outermost loop moves on to a new set of 2048×2048 of tiles. The RISC‑V Zihintntl extension (Non-Temporal Locality Hints) might be used before C tile vector loads and stores, in particular the NTL.PALL instruction. Tiling A and B for the cache hierarchy is likely to save considerable energy. With care and sufficient associativity, it may even be possible to have the A and B tiles occupy the entire LLC, not just half, enabling a 8 MiB LLC to be useful for 2048×2048 last level tiles.

Another tiling consideration is sharing. A LLC cache shared by multiple processors may suggest tiling appropriate to the fraction of the processors sharing the cache if all processors are very active. However, if the processors are working on matrix multiply in parallel, then it may be appropriate to arrange them to be working on different C tiles that share A or B tiles with the other processors.

Still another tiling consideration is prefetching. While processing A and B tiles, it may be advantageous to prefetch the next A and B tiles, so that the computation proceeds in a pipelined fashion. In this case it is appropriate to use half the cache for the working tiles and half for the next tiles. This assumes that the L3 cache has sufficient bandwidth to supply the L2 with data and write the data prefetched from main memory.

Tile Sizes for L3
L3	SEW	EEW	C			A			B			A+B
2 MiB	8	32	1024×1024	4 MiB	200%	1024×1024	1 MiB	50%	1024×1024	1 MiB	50%	2 MiB	100%
2 MiB	16	32	1024×1024	4 MiB	200%	1024×512	1 MiB	50%	512×1024	1 MiB	50%	2 MiB	100%
2 MiB	32	32	512×512	1 MiB	50%	512×512	1 MiB	50%	512×512	1 MiB	50%	2 MiB	100%
2 MiB	32	64	512×512	2 MiB	100%	512×512	1 MiB	50%	512×512	1 MiB	50%	2 MiB	100%
2 MiB	64	64	512×512	2 MiB	100%	512×256	1 MiB	50%	256×512	1 MiB	50%	2 MiB	100%
4 MiB	8	32	2048×2048	16 MiB	400%	2048×1024	2 MiB	50%	1024×2048	2 MiB	50%	4 MiB	100%
4 MiB	16	32	1024×1024	4 MiB	100%	1024×1024	2 MiB	50%	1024×1024	2 MiB	50%	4 MiB	100%
4 MiB	32	32	1024×1024	4 MiB	100%	1024×512	2 MiB	50%	512×1024	2 MiB	50%	4 MiB	100%
4 MiB	32	64	1024×1024	8 MiB	200%	1024×512	2 MiB	50%	512×1024	2 MiB	50%	4 MiB	100%
4 MiB	64	64	512×512	2 MiB	50%	512×512	2 MiB	50%	512×512	2 MiB	50%	4 MiB	100%
8 MiB	8	32	2048×2048	16 MiB	200%	2048×2048	4 MiB	50%	2048×2048	4 MiB	50%	8 MiB	100%
8 MiB	16	32	2048×2048	16 MiB	200%	2048×1024	4 MiB	50%	1024×2048	4 MiB	50%	8 MiB	100%
8 MiB	32	32	1024×1024	4 MiB	50%	1024×1024	4 MiB	50%	1024×1024	4 MiB	50%	8 MiB	100%
8 MiB	32	64	1024×1024	8 MiB	100%	1024×1024	4 MiB	50%	1024×1024	4 MiB	50%	8 MiB	100%
8 MiB	64	64	1024×1024	8 MiB	100%	1024×512	4 MiB	50%	512×1024	4 MiB	50%	8 MiB	100%
16 MiB	8	32	4096×4096	64 MiB	400%	4096×2048	8 MiB	50%	2048×4096	8 MiB	50%	16 MiB	100%
16 MiB	16	32	2048×2048	16 MiB	100%	2048×2048	8 MiB	50%	2048×2048	8 MiB	50%	16 MiB	100%
16 MiB	32	32	2048×2048	16 MiB	100%	2048×1024	8 MiB	50%	1024×2048	8 MiB	50%	16 MiB	100%
16 MiB	32	64	2048×2048	32 MiB	200%	2048×1024	8 MiB	50%	1024×2048	8 MiB	50%	16 MiB	100%
16 MiB	64	64	1024×1024	8 MiB	50%	1024×1024	8 MiB	50%	1024×1024	8 MiB	50%	16 MiB	100%

L2 caches tend to be 256 KiB, 512 KiB, or 1 MiB. For 8-bit data, with sufficient associativity, this will hold A and B matrixes of 512×256, 512×512, and 1024×512 elements at 100% utilization respectively. For 32×32 outer products, this means 8, 16, or 32 vector loads per L2 cache block fill. For 64×64 outer products, this is 4, 8, or 16 loads, which represents reasonable energy savings for the outer product coupled with L2 tiling. With L3 tiles of 2048×2048, each L3 cache block is filled into the L2 2048/256=8 times or 2048/512=4 times.

The same L3 prefetching consideration applies to L2 tiling. Since the suggested outer product configuration matches compute to load bandwidth, the L2 may be read every cycle. Thus some sort of banking may be required to provide bandwidth for data prefetched from the L3 to be written to the L2 for the next tiles.

Tile Sizes for L2
L2	SEW	EEW	C			A			B			A+B
256 KiB	8	32	512×512	1 MiB	400%	512×256	128 KiB	50%	256×512	128 KiB	50%	256 KiB	100%
256 KiB	16	32	256×256	256 KiB	100%	256×256	128 KiB	50%	256×256	128 KiB	50%	256 KiB	100%
256 KiB	32	32	256×256	256 KiB	100%	256×128	128 KiB	50%	128×256	128 KiB	50%	256 KiB	100%
256 KiB	32	64	256×256	512 KiB	200%	256×128	128 KiB	50%	128×256	128 KiB	50%	256 KiB	100%
256 KiB	64	64	128×128	128 KiB	50%	128×128	128 KiB	50%	128×128	128 KiB	50%	256 KiB	100%
512 KiB	8	32	512×512	1 MiB	200%	512×512	256 KiB	50%	512×512	256 KiB	50%	512 KiB	100%
512 KiB	16	32	512×512	1 MiB	200%	512×256	256 KiB	50%	256×512	256 KiB	50%	512 KiB	100%
512 KiB	32	32	256×256	256 KiB	50%	256×256	256 KiB	50%	256×256	256 KiB	50%	512 KiB	100%
512 KiB	32	64	256×256	512 KiB	100%	256×256	256 KiB	50%	256×256	256 KiB	50%	512 KiB	100%
512 KiB	64	64	256×256	512 KiB	100%	256×128	256 KiB	50%	128×256	256 KiB	50%	512 KiB	100%
1 MiB	8	32	1024×1024	4 MiB	400%	1024×512	512 KiB	50%	512×1024	512 KiB	50%	1 MiB	100%
1 MiB	16	32	512×512	1 MiB	100%	512×512	512 KiB	50%	512×512	512 KiB	50%	1 MiB	100%
1 MiB	32	32	512×512	1 MiB	100%	512×256	512 KiB	50%	256×512	512 KiB	50%	1 MiB	100%
1 MiB	32	64	512×512	2 MiB	200%	512×256	512 KiB	50%	256×512	512 KiB	50%	1 MiB	100%
1 MiB	64	64	256×256	512 KiB	50%	256×256	512 KiB	50%	256×256	512 KiB	50%	1 MiB	100%

Prefetching

Program or compiler directed prefetching may be difficult to interleave with computation. Hardware prefetching based on cache misses occurs too late since the goal is to fetch well ahead of the first miss. Also, simple hardware prefetching may not be able to match the requirements of fetching matrix tiles from main memory, given that the pattern in virtual memory would be ⌈TC/CB⌉ blocks from addresses separated by the number of bytes in a row. A hybrid approach may be able to address the needs of matrix prefetch. Software might program the virtual address of the start, and the number of columns, and the stride between rows, and then a prefetch engine would initiate prefetch based on this specification in parallel with computation, presuming that there is sufficient cache and TLB bandwidth for both. Separate prefetch data structures may be needed for each level of the cache hierarchy used by matrix operations.

Software would program such a prefetch engine with virtual addresses, which would need to be translated. This might present a challenge for a Last Level Cache (LLC) that is shared by multiple processors, as the LLC would not have its own translation. Instead the prefetches for the LLC would have to come from the processors, where translation is available. In this case, some sort of coordination is required to avoid redundant prefetch.

Another possibility is to perform simple transformation when reading from one level of the memory hierarchy and writing a lower level. One transformation might be transposing the matrix data (e.g. of the B matrix so that it can be accessed with non-strided loads), or of data expansion (e.g. converting block scaled values to a wider format after scaling). Such transformations would be to a new address, and so would look more like DMA than prefetch. In such cases the target tile would likely be compact, rather than having a large stride between rows, to reduce associativity requirements.

An alternative method in a multiprocessor system would be to use one processor to initiate the prefetches (e.g. with explicit single cache block instructions) on behalf of the other processors. For example, in a 4 processor subsystem, one processor might be responsible for prefetch while three are performing the calculations. The vector and matrix units of the fourth processor would be wasted, however, which may favor the software-directed hardware prefetch described above. In the case of a multi-threaded processor, one thread might be used for prefetch on behalf of the others.

Parallel Processing

Even with a large outer product array, large matrix multiplications are likely to benefit from using multiple processors in parallel. Very little synchronization is strictly necessary because the data shared is all read-only. (It will help to make sure tiles of C are all cache-block aligned to prevent false sharing.) However, when groups of processors share a cache (e.g. the Last Level Cache (LLC)), it is appropriate to share some of the tiles being processed in parallel. For example, 4 processors sharing a L3 cache could all work on C tiles in the same row but different columns, which would allow the L3 to have one copy of the A tiles of that row while each processor works on different column of C, and thus column of B. This may make some synchronization worthwhile, so that one processor is not getting ahead on tiles of A, and therefore causing other processors to miss. Synchronization with prefetching processors or threads will also be required.

In the case of a prefetch processor/thread, computation processors/threads may move on to the next C tile as soon as they finish the current one because the prefetch is already filling reserved cache space for the next tiles, but should not move on to a C tile that would displace A and B tiles that are still being worked on by other processors. Thus processors may get one C tile ahead of others, but not two ahead. A simple barrier synchronization method would be for each processor to increment its own C tile completion count, then then wait for the counts of the prefetch processor/thread proceeding to reach its level minus one as illustrated by the following C snippet (atomic operations not required):

    uint64_t localcount;			// stack variable local to thread
    uint32_t myid;				// my thread index
    volatile uint64_t tilecount[NTHREAD*8];	// one tilecount per cache block
    ⋮
    localcount += 1;
    tilecount[myid*8] = localcount;		// store to show others where we are
    for (size_t i = 0; i != NTHREAD; i += 1) {
      while (tilecount[i*8] < localcount-1);	// wait for others to catch up
    } // for i

Moving Outside the Vector Unit

Going from vectors to an outer product multiply/add array with accumulators for tiles allows the implementation to bring significantly more multiply/add units to bear on matrix multiply. We have already seen how to match computation to load bandwidth by providing a large array of multiply/add units (e.g. 32×16 Δ=2 BF16 multiply/add units for a load bandwidth of 512 bits per cycle). To employ 2048 BF16 units instead of 512, it is necessary to double the vector load bandwidth to 1024 bits per cycle, which is possible, but may not be appropriate for the rest of the unit. Moving matrix computation out of the vector unit, with the bandwidth appropriate there is one possibility being explored in the proposed Attached Matrix Extension (AME), but AME only makes sense when the bandwidth to it can be significantly increased relative to the vector unit. AME is still probably best built around outer product arrays sized to the load bandwidth, but for some incremental increase in load bandwidth. For example, it might benefit from a direct connection to HBM3E memory (see below). Even if AME is located outside of a single processor core for such reasons, it still makes sense for it to be built on top of the RISC‑V Vector (RVV) instruction set. If the RVV is too complex for some implementations, a simplified subset (e.g. omitting segmented loads) can be defined as the basis for AME. RVV instructions would be sent to AME for execution, but this would be transparent to software. One avenue for further investigation is whether AME might be able to source from local SRAM storage for one or both matrixes. Local storage of one matrix that will be used multiple times would double the computation rate possible, which may not seem like much, but the energy efficiency might justify it. A unique way to increase bandwidth and save power might be to have SRAM storage located at each node of the outer product array, if an application for such can be found. For example, it might be reasonable to have about 2048 bits of SRAM per tile element (e.g. 256 KiB total for a 32×32 tile array). Whether there is an application for such a configuration is the question; I suspect it is probably too small to be useful. More likely, AME might employ SRAM for tiling as described above, e.g. to hold a 4096×4096 tile of A in one SRAM and a 4096×4096 tile of B in another. For FP8 data, each SRAM might be 32 MiB to allow the next 4096×4096 tile to be read in parallel with doing outer product operations on the previous read. One challenge in such an approach is keeping the reads from DRAM to this SRAM coherent with the rest of the system, given the data rates involved.

Keeping up with High Bandwidth Memory

The HBM3E generation of DRAM promises to deliver 1.2 terabytes per second (TB/s). It is interesting to ask what sort of outer product array would be matched to this bandwidth. For a 4 GHz processor, this bandwidth is 300 bytes per cycle. Given the difficulties of hitting peak bandwidth and the appropriateness of powers of two, call this 256 bytes (2048 bits) per cycle. For BF16 data, this calls for a 128×64 Δ=2 outer product array, or for a quad-core with each processor utilizing a 64×32 array. This is feasible in 2024 process nodes using the techniques proposed here. For int8 and fp8 data, 256×128 arrays are required. For 8-bit data, the 256×128 array delivers 65 TOPS/GHz; for example, 262 TOPS at 4 GHz.

		<webmaster at securerisc.org>
2024-11-28

Proposal for RISC‑V Matrix

Glossary

Table of Contents

Matrix Multiply

Matrix Algebra

Matrix Multiply Using Vectors

Matrix Multiply Using An Outer Product Array

Matrix Accumulators

Making Outer Product Scalable

Specifics of the Proposal

Extra Accumulators

Below the Load Bandwidth Limit

Full Accumulator Array Reduced Multipliers

Reduced Accumulator and Multiplier Arrays

Open Issues

Other Methods

Avoiding Accumulators

Matrixes in the Vector Register File

Inner Product Methods

Comparison of Methods

Other Operations

Matrix × Vector

Matrix × Vector using RISC‑V Vector

Matrix × Vector using Accumulators

Batched Matrix × Vector

Matrix Transpose

Widening

Matrix Addition, Subtraction, Scaling

Convolution

Motion Search

Tiling for the Cache Hierarchy

Prefetching

Parallel Processing

Moving Outside the Vector Unit

Keeping up with High Bandwidth Memory